Перемычку при горизонтальном непроницаемом основании

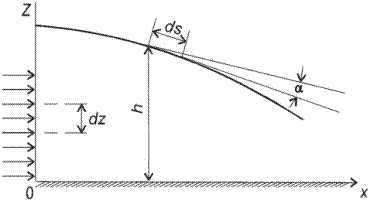
Безнапорное движение жидкости встречается также при шахтной добыче нефти, в условиях гравитационного режима и вследствие истощения пластовой энергии, когда уровень жидкости (свободная поверхность) оказывается ниже кровли пласта.

Для инженерных расчетов пользуются гидравлической теорией безнапорного движения, которая является неправильной. Однако расчетные данные для дебитов хорошо совпадают с экспериментальными результатами. В описании же свободной поверхности в приближенной гидравлической теории имеется большая погрешность, так как не учитывается промежуток высачивания ВС (см. рис. 5.1).

Введем некоторые понятия. Уровень Н ₁ называется верхним бьефом, уровень Н ₂ – нижним бьефом; ВС – промежуток высачивания, через который жидкость сочится в атмосферу и стекает в нижний бьеф. Поверхность ABC представляет собой пьезометрическую (депрессионную) поверхность. Свободная поверхность АВ всегда выходит выше нижнего бьефа. Те же самые понятия остаются и для безнапорного притока к колодцу.

Основная трудность точного решения задач безнапорного движения состоит в том, что неизвестна форма области движения жидкости, тогда как при напорной фильтрации она известна, поскольку кровля и подошва фиксированы.

Некоторые точные решения для безнапорного движения через прямоугольную перемычку выполнены П. Я. Полубариновой-Кочиной. Для притока к колодцу до сих пор точного решения не имеется.

Рассмотрим приближенную гидравлическую теорию. Проведем произвольное вертикальное сечение в безнапорном потоке (рис. 5.3), где h есть ордината точки свободной поверхности в данном сечении, i – Sin a –уклон свободной поверхности. Делаются следующие допущения: 1) горизонтальные компоненты скорости распределены равномерно; 2) давление вдоль вертикали распределено по гидрастатическому закону, т. е. 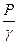«напор» Н = Z + = Н (х, z). «Напор», таким образом, вдоль каждой вертикали предполагается постоянным. Эти предпосылки допустимы в тех областях течения, где i ²<<l и кривизна линии тока меньше i, т. е. вдали от промежутка высачивания (i» 1). Будем считать, что над свободной поверхностью Р = Р _ат, т. е. избыточное давление равно нулю. Принимая за избыточное давление р =0, находим, что «напор» Н равен глубине потока h, т. е. Н = h, откуда по закону Дарси следует выражение для поверхностной скорости фильтрации

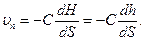(5.1)