Жидкости к прямолинейной галерее.
Для вычисления этого интеграла воспользуемся зависимостью [5]:
где g0 и т 0 – удельный вес жидкости и коэффициент пористости при начальном пластовом давлении Р 0; Р – текущее пластовое давление; b* – коэффициент упругоемкости. Здесь произведение (gт) распределяется по длине пласта так же, как и давление Р (см. рис.7.1б). Площадь заштрихованного треугольника дает нам вес жидкости в элементе площади по длине l
Если g есть весовой расход жидкости, тогда для количества жидкости G можно записать
откуда следует:
В соответсвии с законом Дарси весовой расход определяется формулой
Продифференцируем уравнение (7.4) по времени, учитывая при этом (7.5) и (7.6):
В соответствии с (7.3), имеем:
Подставив (7.8) в (7.7), находим:
Принимая g с »γ;0 (так как величина коэффициента сжимаемости для жидкости мала) и m ≈m 0= соnst, получим
или
откуда имеем
Формула (7.9) выражает закон движения условной зоны депрессии. Определим объемный расход жидкости на единицу площади пласта (f =1) или, что то же самое, скорость фильтрации:
Учитывая (7.9), находим
Для сравнения запишем точную формулу для объемного расхода [5]
где æ; – коэффициент пьезопроводности. Нетрудно установить, что погрешность формулы (7.11) составляет около 11%. Рассмотрим теперь ту же задачу, но при этом пусть задан дебит q = const. Рассчитаем депрессию. Подставляя (7.8) в (7.4) и принимая g к@ g с, находим объем отобранной жидкости за время t
Подставляя значение l (t) из формулы (7.10) в (7.13), получаем
Погрешность приближенной формулы (7.14) составляет около 25%. Подставив (7.14) в (7.10), после некоторых преобразований получим
Но так как q = const, то Q=qt. Следовательно,
При заданной депрессии имеем формулу (7.9). Таким образом, при заданной депрессии метод последовательной смены стационарных состояний дает результаты с меньшей погрешностью, чем при заданном расходе.
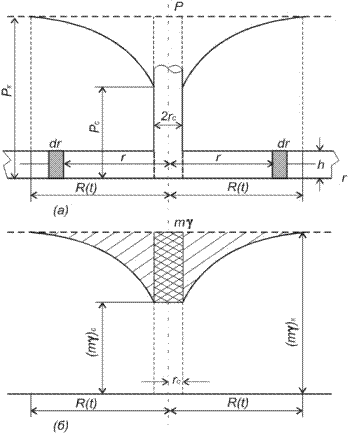
7.2.2. Расчет плоско-радиального притока упругой жидкости. Рассмотрим плоскорадиальный приток упругой жидкости к скважине из пласта толщиной h (рис. 7.2). После того, как скважина пущена в работу и отбирает жидкость из пласта, вокруг нее образуется воронка депрессии, т. е. зона пониженного давления, которая теоретически охватывает весь пласт. Приближение в решении задачи заключается в том, что мы последовательно во времени фиксируем радиус воронки депрессии, т. е. в каждый момент времени радиус воронки R (t) принимается как конечная величина. При этом кривая распределения давления аппроксимируется логарифмической кривой, тогда как при прямолинейном движении с двухсторонним питанием она аппроксимируется двумя прямыми. Поэтому точность приближенного метода для плоскорадиального притока будет выше. Выделим в пласте элементарное кольцо шириной dr на расстоянии r от оси скважины (см. рис. 7.2). Очевидно, вес жидкости в начальный и данный моменты определится соответственно выражениями:
Отобранное количество жидкости за время t из элемента составит
Рис. 7.2. Схема к расчету неустановившегося плоско-радиального притока сжимаемой жидкости по методу последовательной смены стационарных состояний
Вес отобранной жидкости из пласта определится интегралом
Чтобы вычислить интеграл (7.16), надо знать закон изменения (тg). Известно, что при стационарном плоскорадиальном притоке несжимаемой жидкости давление в окрестности скважины распределяется по логарифмическому закону:
Но так как (тg) можно выразить в соответствии с (7.17) формулой
тогда следует
Подставляя (7.18) в (7.16), получаем
Интеграл в (7.19) можно взять по частям:
После соответствующего преобразования из (7.19) получаем
Учтем и жидкость, отобранную из скважины при снижении давления от Р к до Р с (на рис. 7.2 двойная штриховка). Это количество жидкости выразится формулой
С учетом (7.8) и принимая gк»gс, суммарный отбор жидкости
Теперь найдем связь между средним давлением в пласте
Сравнивая (7.22) и (7.23), устанавливаем
При R (t)>> r с и малой величине депрессии D Р = Р к– Р с из формулы (7.24) следует: Исследуем уравнение (7.22) и найдем закон расширения воронки депрессии. При пуске скважины в эксплуатацию, как упоминалось ранее, происходит непрерывное расширение воронки депрессии. Период, за который воронка депрессии достигает границы пласта, называется первой фазой неустановившегося движения (первая фаза истощения залежи), после чего начинается II фаза упругого режима (вторая фаза истощения). При этом предполагается стационарное движение жидкости во всем пласте. Если граница резервуара является контуром пласта, где поддерживается постоянное давление (например, линия нагнетания), то II фазу можно рассматривать как стационарный режим. Рассмотрим I фазу упругого режима. Из формулы Дюпюи, которую мы считаем справедливой в случае неустановившегося притока для каждого момента времени t, имеем
Подставляя (7.25) в (7.22), находим
Из (7.26) следует
Подставляя значение (7.27) в формулу Дюпюи (7.25), находим депрессию при q = const.
Если R (t)>> r c, то (7.24) принимает вид
Погрешность формулы (7.29) по сравнению с точным решением составляет порядка 6%. Если задана постоянная депрессия D Р = const, то принцип исследования остается тем же самым, что и при q = const. При этом можно использовать формулу (7.29) для расчета расширения воронки депрессии. Погрешность составит 10-15%. Вторую фазу истощения можно исследовать аналогично.
|

 (7.3)
(7.3)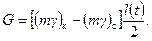 (7.4)
(7.4)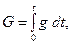
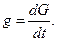 (7.5)
(7.5)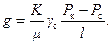 (7.6)
(7.6) (7.7)
(7.7)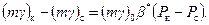 (7.8)
(7.8)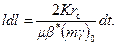

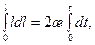
 , æ;=
, æ;= 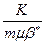 . (7.9)
. (7.9)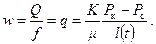 (7.10)
(7.10)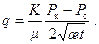 (7.11)
(7.11)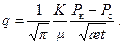 (7.12)
(7.12)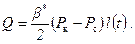 (7.13)
(7.13)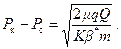 (7.14)
(7.14)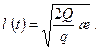
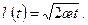 (7.15)
(7.15)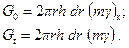
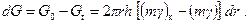
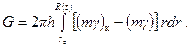 (7.16)
(7.16)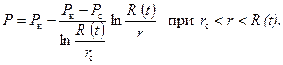 (7.17)
(7.17)
 (7.18)
(7.18) (7.19)
(7.19)
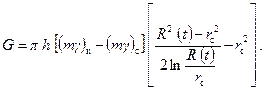 (7.20)
(7.20)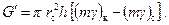 (7.21)
(7.21)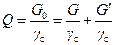 выразится формулой
выразится формулой (7.22)
(7.22)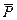 и Р к. Предположим, что всюду в пласте давление снизилось равномерно. Тогда отобранный объем жидкости при упругом расширении составит
и Р к. Предположим, что всюду в пласте давление снизилось равномерно. Тогда отобранный объем жидкости при упругом расширении составит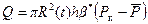 (7.23)
(7.23)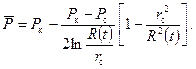 (7.24)
(7.24) (7.25)
(7.25)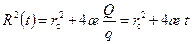 (7.26)
(7.26)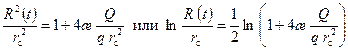 (7.27)
(7.27)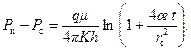 (7.28)
(7.28)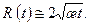 (7.29)
(7.29)


