Утверждено Редакционно-издательским советом университета в качестве учебно-методического пособия 3 страница
или
Найдем w4 через передаточную функцию механизма:
Варьируя значения входных угловых скоростей wН и w1, а также их направления (знаки), всегда можно определить по величине и направлению действительную скорость w4 выходного вала исследуемого механизма. Задавая угловую скорость w1 равной нулю (планетарный механизм с одним неподвижным центральным колесом 2 ¢), получаем
или передаточное отношение планетарного механизма
Другой способ определения взаимосвязи угловых скоростей дифференциального механизма – графический. Точность этого метода ниже, чем у метода Виллиса, и существенно зависит от точности геометрических построений. Рассмотрим применение графического метода на примере того же дифференциального механизма (рис. 3.6). Зададим точке А зубчатого колеса 1 произвольную скорость VА и изобразим ее вектором на плане скоростей рис. 3.6, б, откладывая его влево от вертикальной оси нулевых скоростей – положительное направление вращения. Ось вращения колеса 1 остается неподвижной, следовательно, точка О 1, лежащая на этой оси, имеет скорость, равную нулю, и на плане скоростей располагается на вертикальной нулевой линии. Прямая, соединяющая точку О 1 и конец вектора VА на плане, является линией концов векторов скоростей точек колеса 1, лежащих на его радиусе, и называется диаграммой скоростей точек звена 1. Точка А принадлежит одновременно и колесу 2, следовательно, оно имеет в этой точке ту же скорость, а точка О 2 на его оси неподвижна. Проведем через точки конца вектора VА и О 2 на плане скоростей прямую до пересечения с линией направления вектора скорости VВ, принадлежащей тому же звену, что и колесо 2. Эта прямая является диаграммой скоростей звена 2. Теперь зададим точке С водила, лежащей на оси вращения сателлитов, произвольную скорость VС, направленную противоположно скорости VА (отрицательное вращение), и, соединив прямой концы векторов скоростей VB и VC, получим диаграмму скоростей радиальных точек блока сателлитов. По этой диаграмме найдем положение конца вектора скорости VD, которую будет иметь точка D, принадлежащая и сателлиту 3 ¢ и колесу 4. Соединив конец вектора скорости VD с точкой О 2 на плане скоростей, получим диаграмму скоростей радиальных точек колеса 4. Перейдем к угловым скоростям вращения колес механизма. Известно, что линейные скорости точек пропорциональны их расстоянию от центра вращения Выразим скорости точек зубчатых зацеплений через радиусы и углы диаграммы скоростей: 1) 2) 3) 4) Решая полученную систему алгебраических уравнений совместно, получаем выражение для тангенса угла диаграммы скоростей выходного звена:
Поскольку при одинаковом модуле зацепления радиус делительной окружности колеса равен Рассмотрим порядок исследования графическим методом более простого планетарного механизма, для чего зададим tg φ1 = 0. Тогда в общем случае
а передаточное отношение
Это отношение можно определить и чисто графически, построив план угловых скоростей. Для этого проведем горизонтальную линию (см. рис. 3.6, г) и из произвольного полюса Р опустим на нее перпендикуляр h. Затем из полюса Р под углом j Н и j4 проведем две прямые до пересечения с горизонталью. Получили два прямоугольных треугольника РОА и РОВ, с углами у вершин j Н и j4 соответственно и общим прилегающим катетом РО = h. Следовательно, отношение тангенсов углов будет определяться отношением противолежащих катетов:
Порядок выполнения лабораторной работы 1. Разработать и вычертить в масштабе кинематическую схему исследуемого зубчатого механизма. Обозначить порядковым номером каждое из зубчатых колес механизма. Справа от схемы оставить место для построения плана скоростей. 2. Составить таблицу чисел зубьев колес, взяв данные, указанные на макете зубчатого механизма.
3. Выделить и классифицировать все кинематические пары и звенья, входящие в состав механизма, определить его степень подвижности. 4. Определить передаточное отношение сложного зубчатого механизма аналитическим методом мысленного останова водила (метод Виллиса). 5. Определить передаточное отношение этого же механизма графическим методом, построив план скоростей точек звеньев. 6. Проверить полученные результаты экспериментально, для этого входной вал повернуть на n вх оборотов, одновременно отсчитывая число оборотов n вых, которое совершит выходной вал. Их отношение
7. Сформулировать вывод о проделанной работе и достижении поставленных целей. Вопросы для самоконтроля 1. В чем заключается физический смысл метода Виллиса? 2. Как определить степень подвижности механизма? 3. Что такое передаточное отношение, передаточная функция? 4. В чем отличие дифференциального и планетарного механизмов? 5. Назвать основные звенья дифференциального механизма. 6. Назвать основные классификационные признаки зубчатых механизмов. 7. Порядок построения плана скоростей точек звеньев. 8. Что такое план угловых скоростей звеньев? 9. В чем отличие рядового и ступенчатого зубчатых механизмов? 10. Каким образом можно выразить угловую скорость через план линейных скоростей точек звена?
Лабораторная работа № 4 Изучение методов изготовления Цель работы 1. Изучение теории зубчатого зацепления. 2. Освоение геометрии зубчатых колес. 3. Исследование возможностей улучшения нагрузочных характеристик зубчатых колес. 4. Изучение способов изготовления зубчатых колес. Основные сведения Основы теории зацепления зубчатых механизмов Назначение зубчатых механизмов – обеспечить непрерывную передачу вращения от одного колеса к другому. Это условие выполняется, если соблюдается постоянство передаточного отношения Основная теорема зацепления Основная теорема зацепления (Виллиса) гласит: Общая нормаль в точке контакта сопряженных профилей в любой момент взаимодействия должна проходить через полюс зацепления, положение которого на межосевой линии делит ее на отрезки, обратно пропорциональные скоростям вращения колес, участвующих в зацеплении, т. е.
где О 1, О 2 – центры вращения соответственно шестерни и зубчатого колеса, а О 1 О 2 – межцентровое (межосевое) расстояние; Р – полюс зацепления (рис. 4.1). Профили зубьев, удовлетворяющие требованию основной теоремы зацепления, называются сопряженными. Таких профилей можно подобрать довольно много, но широкое распространение в машиностроении и приборостроении нашли предложенные Эйлером – эвольвенты.
Рис. 4.1. Взаимодействие двух эвольвент Эвольвента и ее свойства Эвольвентой называется кривая, которая описывается точкой прямой линии Прямая линия Геометрическое место центров кривизны любой кривой (эвольвенты) называется эволютой. Эвольвенту и эволюту характеризуют следующие геометрические свойства: · эвольвента начинается на основной окружности и всегда находится вне ее; · эвольвента является разверткой эволюты, т.е. она описывается точкой прямой, которая перекатывается по эволюте без скольжения, поэтому радиус кривизны эвольвенты равен длине соответствующей дуги эволюты; · касательная к эволюте является нормалью к эвольвенте; · точка касания с эволютой нормали к эвольвенте является центром ее кривизны.
Образование эвольвенты характеризуется следующими параметрами: радиусом-вектором R, радиусом основной окружности Длина отрезка производящей прямой равна длине дуги окружности, заключенной в пределах углов
Длину производящей прямой
Приравняв правые части уравнений и сделав математические преобразования, определим угол поворота радиуса-вектора:
Величина угла
Из треугольника ОЕР определяем величину радиуса-вектора:
Радиус кривизны эвольвенты, начиная с точки А, является переменной величиной, в любой точке эвольвенты он соответствует длине производящей прямой b, которая определяется по формуле
Эвольвентные профили зубьев цилиндрических колес внешнего и внутреннего зацепления строятся от общей основной окружности (рис. 4.3). Расстояние между двумя соседними эвольвентами, измеренное по касательной к основной окружности является постоянным. Оно равно длине дуги основной окружности, заключенной между начальными точками А 1, А 2, А 3, …, АS двух соседних эвольвент, и называется основным шагом:
где Если одна эвольвента (рис. 4.4), вращаясь с постоянной угловой скоростью, воздействует на другую эвольвенту, то она будет сообщать ей также постоянную угловую скорость независимо от расстояния
Таблица значений
вращения двух эвольвент, действующих одна на другую, будет обратно пропорционально радиусам их основных окружностей:
Это отношение называют передаточным отношением. Основные геометрические параметры, Понятия и термины, относящиеся к геометрии и кинематике зубчатых передач, стандартизованы. Стандартами устанавливаются термины, определения и обозначения, а также методы расчета геометрических параметров. Напомним, что меньшее из пары зубчатых колес называют шестерней, а большее – колесом. Параметрам шестерни приписывают индекс 1, а параметрам колеса – 2 (рис. 4.4). Передаточным числом называют отношение числа зубьев колеса к числу зубьев шестерни.
Касание двух взаимодействующих эвольвент происходит только на общей касательной Е 1 Е 2 к их основным окружностям. Общая касательная к двум основным окружностям называется линией зацепления. Участок линии зацепления, ограниченный окружностями вершин зубьев Любая точка линии зацепления может быть полюсом зацепления Р. Угол, образованный общей касательной к двум основным окружностям и перпендикуляром к линии их центров, называется углом зацепления Относительное движение двух эвольвент может быть представлено цилиндрами, вращающимися относительно друг друга посредством трения, без скольжения. Такие цилиндры называются начальными, а их диаметры – диаметрами начальных окружностей (dw 1 и dw 2). У сопряженной пары некоррегированных зубчатых колес, работающих при правильном межосевом расстоянии, делительные окружности совпадают с начальными.
Рис. 4.4. Геометрические параметры зубчатой передачи
Делительная окружность – параметр, введенный для удобства в расчетах, определяемый через модуль и число зубьев колес:
Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают. Модуль – это часть диаметра делительной окружности, приходящаяся на один зуб колеса (мм):
Модуль чаще определяется как отношение шага р по делительной окружности к числу π:
Ряд модулей, применяемых для цилиндрических, шевронных, конических и червячных передач, стандартизован (ГОСТ 9563–60). Исходным контуром называется контур зубчатой рейки в нормальном к направлению зубьев сечении. Исходный контур для цилиндрических колес внешнего и внутреннего зацепления представляет собой зубчатую рейку с прямолинейным профилем в пределах глубины захода
|
,
.
.
.
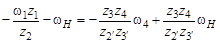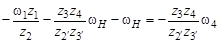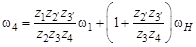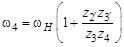
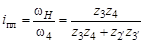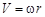. Следовательно, угловая скорость 
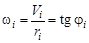, что на плане скоростей соответствует тангенсу угла наклона tg φ i диаграммы скоростей i -го звена к вертикальной оси, по которой откладывается расстояние r от центра вращения до точки, имеющей соответствующую линейную скорость.
;
;
;
.
.
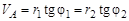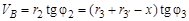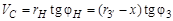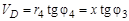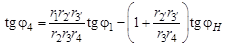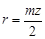, тангенсы углов равны угловым скоростям звеньев, а знак (–) определяется отрицательной скоростью водила – w Н, полученное выражение полностью аналогично уравнению по методу Виллиса.
,
.
.
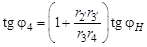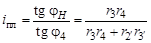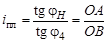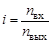определит передаточное отношение механизма. Эксперимент повторить три раза при различных n вх. Результаты оформить в таблицу.
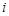= const). Постоянное передаточное отношение в зубчатом механизме обеспечивается за счет правильного подбора профилей соприкасающихся зубьев. Условия, которым должны отвечать кривые, очерчивающие профили зубьев зубчатых колес, определяет основная теорема зацепления.
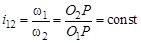, (4.1)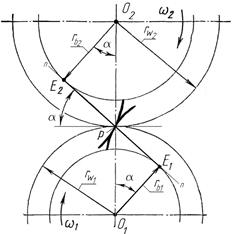
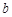(рис. 4.2), при перекатывании последней по основной окружности 
.
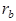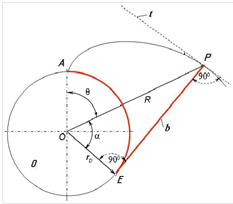
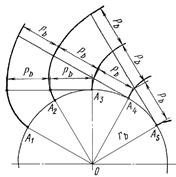
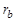, углом поворота 
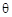радиуса-вектора R и углом давления.
:
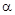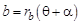. (4.2)
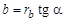. (4.3)
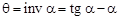. (4.4)
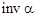(читается «инволюта»), значения инволют табулированы и приведены в табл. 4.1. Без помощи таблиц эвольвентную функцию можно определить по формуле
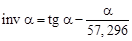. (4.5)
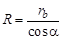. (4.6)
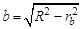. (4.7)
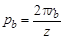, (4.8)
– число зубьев.
Т а б л и ц а 4.1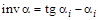
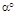
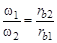. (4.9)
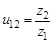. (4.10)
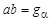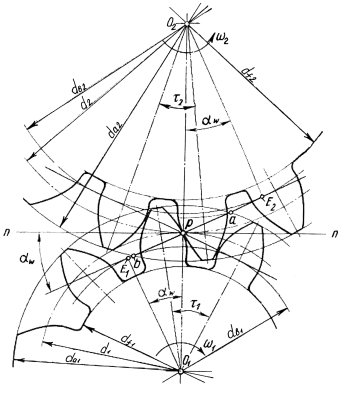
, называется активной линией зацепления.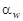
.
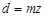. (4.11)
.
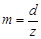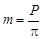. (4.12)
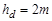(рис. 4.5). Под глубиной захода понимается высота зуба, которая участвует в работе.
