Определение приведенного коэффициента трения и коэффициента полезного действия (КПД) винтовой пары.
Общие сведения
Существуют трение скольжения и трение качения. Трение скольжения имеет место при относительном движении двух тел, скорости которых в точках касания различны. Трение качения возникает в высших кинематических парах, скорости которых в точках касания одинаковы по величине и направлению. Различают два вида сил трения скольжения: сила трения при покое и сила трения при движении. Трение скольжения при покое При попытке сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения (или сила сцепления), которая может принимать любые значения от нуля до величины F пp,называемой предельной силой трения. Экспериментально коэффициент трения можно найти с помощью прибора (рис. 5.1). Горизонтальная плита АВ и прямоугольный брус С изготавливаются из материалов, для которых определяется коэффициент трения покоя. На брус С будут действовать сила тяжести Q, уравновешенная нормальной реакцией плиты N, и сдвигающая сила F, которая при
Рис. 5.1. Определение коэффициента
покое уравновешивается силой трения F т(сила F численно равна весу груза). Меняя грузы, находим нагрузку F *, при которой брус трогается с места. Проделав ряд опытов, можно убедиться, что при изменении силы тяжести Q бруса С величина F * возрастает пропорционально Q. Опыты показывают следующее. 1. Величина предельной силы трения F пp равна произведению коэффициента трения покоя f 0 (статического коэффициента трения) на нормальную реакцию (нормальное давление): F пp = f 0 N. Учитывая, что F пp = F * и N = Q, находим
Для данных условий опыта значение f 0 – величина постоянная. Коэффициент трения покоя f 0 (статический коэффициент трения) определяется опытным путем и зависит от материала соприкасающихся тел и состояния поверхностей (шероховатости, температуры, влажности, наличия смазки и др.). 2. Величина предельной силы трения F пp в широких пределах не зависит от размеров соприкасающихся при трении поверхностей. Объединяя вместе положения А и Б, получаем, что при равновесии сила трения покоя (сила сцепления тела с поверхностью) F т ≤ F пp или F т ≤ f 0 N. Следовательно, пока тело находится в покое, сила трения F т равна сдвигающей силе F, а не величине F пp = f 0 N. Сила трения F тпринимает значение F пp = f 0 N только тогда, когда положение равновесия становится предельным. Реакции шероховатых связей. Угол трения Реакция реальной (шероховатой) связи будет слагаться из двух составляющих: из нормальной реакции N и перпендикулярной к ней силы трения F т.
Так как F пp = f 0 N, имеем tg j0 = f 0. При равновесии реакция шероховатой связи R в зависимости от сдвигающих сил может проходить где угодно внутри угла трения. Когда равновесие становится предельным, реакция R будет отклонена от нормали на угол j0. Сила трения при движении Сила трения направлена в сторону, противоположную движению, и равна произведению динамического коэффициента трения f (далее коэффициент трения) на нормальную реакцию (нормальное давление): F т= f N. Это выражение представляет собой закон Кулона–Амонтона, установленный опытным путем. Значения коэффициента трения f зависят от материала, состояния поверхностей и в некоторой степени от скорости движения тел. В большинстве случаев с повышением скорости величина f сначала несколько убывает, а затем сохраняет почти постоянное значение. Коэффициент трения f = arctg j. Величину jназывают углом трения при движении. Коэффициент трения f определяется опытным путем. Винтовая пара Винтовая пара представляет собой две детали (винт и гайку), соединенные по винтовой поверхности. Винтовую пару используют для преобразования вращательного движения в поступательное, или наоборот. Винтовые пары бывают с треугольным, прямоугольным и круглым профилем винтовой поверхности. В технике винтовую поверхность часто называют резьбой. Резьбы с треугольным профилем подразделяют на метрические, дюймовые, трапецеидальные и упорные.
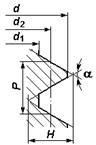
Основные геометрические параметры метрической резьбы по ГОСТ 9150–81 (рис. 5.3): Н – высота исходного профиля (равносторонний треугольник); d, d 2, d 1 – диаметры наружный, средний и внутренний;
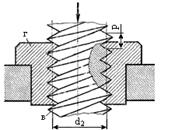
Рис. 5.5. Винтовые пары с прямоугольной и треугольной резьбой: в – винт, г – гайка, Р и d 2 – шаг и средний диаметр резьбы
шаг Р – расстояние между ближайшими сходственными точками контура по линии, параллельной оси резьбы; угол профиля a = 60°; угол подъема винтовой линии резьбы g (рис. 5.4).
Здесь t – период вращательного движения. Период вращательного движения гайки
где w и n – угловая скорость и частота вращения гайки. Скорость поступательного перемещения гайки
Трение в винтовой паре Рассмотрим винтовую пару с прямоугольным профилем резьбы (рис. 5.7). Полагаем, что осевая нагрузка Fа на винт сосредоточена на одном витке и что реакция гайки приложена по средней линии резьбы, т. е. по d 2.
Рис. 5.7. К определению сил трения в винтовой паре
Перемещение гайки по винту можно рассматривать как движение ползуна по наклонной плоскости с углом наклона g (рис. 5.8). При равномерном движение ползуна справедливым является следующее уравнение равновесия:
где Ft = М / r 2 – горизонтальная сила, действующая на ползун (гайку), М – крутящий момент пары сил, приложенных к гайке на расстоянии r 2 от оси винта в плоскости, перпендикулярной оси (в горизонтальной плоскости). Из плана сил (рис. 5.9) видно, что движущая сила Ft, необходимая для равномерного движения ползуна вверх по наклонной плоскости, связана с величиной осевой силы Fа соотношением Ft = Fа tg (g + j), а крутящий момент М пары, приложенный к гайке, будет М = Ft r 2 = Fа tg (g + j) r 2. Из закона Кулона–Амонтона следует F т = f N = N tg j. Из плана сил определим силу трения, действующую в винтовой паре:
Разделив числитель и знаменатель этого выражения на cos jи учитывая, что f = tg j, получим
В винтовой паре с треугольной резьбой нормальная сила N > Fа (рис. 5.10), поэтому сила трения F т больше, чем в рассмотренной выше винтовой паре с прямоугольным профилем резьбы. Соответственно
Рис. 5.10. Соотношения между нормальной
угол трения jи коэффициент трения f увинтовой пары с треугольной резьбой будут больше, чем в винтовой паре с прямоугольным профилем резьбы. В винтовой паре с треугольной резьбой коэффициент и угол трения будут
Полученные для винтовой пары с треугольным профилем резьбы коэффициент f ¢ и угол j¢ трения называются приведенными коэффициентом и углом трения. Коэффициент полезного действия винтовой пары Сравнивая затраты потенциальных энергий при подъеме тела с силой тяжести G = mg по наклонной плоскости (по винтовой линии) без трения и с трением, получим
Рис. 5.11. К определению КПД
где А пол – полезная работа, затрачиваемая на подъем груза по гладкой наклонной поверхности; А затр– работа, затрачиваемая на подъем груза по шероховатой наклонной поверхности треугольного профиля; j¢ – приведенный угол трения. Определение приведенного
В вертикальной стенке плиты 1 выполнена расточка под упорный шарикоподшипник 6, который предназначен для уменьшения трения между торцом гайки 3 и плитой 1. Торец гайки 3 взаимодействует с шарикоподшипником 6 через шайбу 7. При ограничении осевых перемещений элементов винтовой пары (болта и гайки) и при вращении одного из ее элементов (гайки) в винтовой паре возникнет осевая сила Fа. Осевая сила Fа будет вызывать деформацию скобы. Вращение гайки осуществляют динамометрическим ключом (на рисунке не показан), который позволяет контролировать величину крутящего момента М (момента завинчивания), прикладываемого к гайке. Порядок выполнения работы 1. Из условия прочности болта определить верхнюю границу величины осевой силы Fа:
где d 1 – внутренний диаметр резьбы болта (табл. 5.1); [sт] = 200 МПа – предел текучести материала болта; n = 5...10 – коэффициент запаса прочности. 2. Выбрать четыре значения осевой силы Fа, которыми будем нагружать винтовую пару: F 1 = 0,25(Fа)mаx, F 2 = 0,50(Fа)mаx, F 3 = 0,75(Fа)mаx и F 4 = (Fа)mаx. 3. Величины сил, деформирующих скобу (рис. 12), контролировать по показаниям (делениям) D у индикатора часового типа 5, установленного на скобе. Тарировочная зависимость силы от величины деформации скобы F = 396D у, Н. 4. Указанные в п. 2 величины Fа и соответствующие им значения D у занести в табл. 5.2.
Т а б л и ц а 5.1 Некоторые геометрические параметры винтовых пар
* ГОСТ 9150–81; ГОСТ.6958–78.
5. Собрать на экспериментальной установке винтовую пару (болт и гайку). Торец гайки опереть через шайбу на шарикоподшипник. 6. Гайку затянуть от руки. 7. Выставить стрелку индикатора 5 на скобе посредством его смещения относительно скобы. При смещении стрелка должна совершить два оборота. Зафиксировать индикатор винтом (на схеме не показан) и установить «ноль» на подвижной шкале индикатора. 8. Динамометрическим ключом вращать гайку до реализации в винтовой паре осевой силы F 1= 0,25(Fа)mаx. (Перед вращением гайки установить стрелку индикатора динамометрического ключа в нулевое положение.) 9. При достижении F 1 = 0,25(Fа)mаx зафиксировать показания D K индикатора динамометрического ключа и записать их в табл. 5.2. 10. Величину крутящего момента М, прикладываемого к винтовой паре, определить по тарировочной зависимости динамометрического ключа: М = K т × DК, Н × м, где K т = 0,5977; 0,5715; 0,4981 – тарировочные коэффициенты динамометрических ключей № 1, 2 и 3; DК– показания (деления) индикатора динамометрического ключа. 11. Повторить работу в соответствии с пп. 8–10 для значений осевых сил: F 2, F 3 и F 4. 12. Используя значения Fа и М, определить приведенный угол трения j¢ в винтовой паре по формуле
где d 2 – средний диаметр резьбы; g – угол подъема резьбы (табл. 5.1). 13. Определить приведенные коэффициенты трения f ¢ в винтовой паре: f ¢ = tg(j¢). 14. Определить значения коэффициентов полезного действия (КПД) винтовой пары hпо формуле
15. Все опыты повторить три раза. 16. Вычислить средние значения
Т а б л и ц а 5.2 Результаты расчетов
17. Построить графики, иллюстрирующие изменение в винтовой паре средних значений приведенного коэффициента трения 18. Проанализировать результаты и сделать вывод.
0 F 1 F 2 F 3 F 4 Осевая сила Fа
Рис. 5.13. Зависимость
Содержание отчета по работе 1. Цель работы. 2. Схема экспериментальной установки. 3. Результаты экспериментов и расчетов записать в таблицу 2. 4. Зависимости средних значений f ¢ср и hср от осевой силы Fа. 5. Вывод.
Вопросы для самоконтроля 1. Что такое трение? 2. Виды трения. 3. Что является коэффициентом и углом трения? 4. Геометрические параметры винтовой пары (метрической резьбы). 5. Какие силы действуют в винтовой паре и как они связаны между 6. Почему применяют в расчетах винтовых пар приведенный коэффициент трения f '? 7. Приведенный угол трения j ¢ в винтовой паре. 8. Методика расчета приведенного коэффициентатрения f ' в винтовой паре. 9. Методика расчета КПД hвинтовой пары. 10. Дать анализ результатов экспериментов.
ЛАБОРАТОРНАЯ РАБОТА № 6 БАЛАНСИРОВКА ЖЕСТКИХ РОТОРОВ ЦЕЛЬ РАБОТЫ 1. Ознакомление с устройством балансировочного станка. 2. Статическое уравновешивание ротора. 3. Динамическое уравновешивание ротора. ОСНОВНЫЕ СВЕДЕНИЯ Под уравновешиванием вращающихся звеньев понимается задача, связанная с распределением масс по звену для снижения давления на стойку механизма. Простейшей задачей этого типа является задача уравновешивания вращающегося звена, когда полностью или частично устраняются динамические реакции на его опоры, т. е. реакции, зависящие от сил инерции. Для полного устранения этих реакций необходимо, чтобы главный вектор
Иногда ограничиваются выполнением только условия (6.1), которое равносильно условию расположения центра масс на оси вращения звена. Перераспределение массы звена, переводящее его центр масс на ось его вращения, называется статическим уравновешиванием вращающегося звена. Статическое уравновешивание вращающихся звеньев Если условие (6.1) не выполнено, то звено называется статически неуравновешенным. За меру статической неуравновешенности или статического дисбаланса принимают величину статического момента масс звена относительно оси вращения:
Здесь Неуравновешенность в рассматриваемом случае называется статической, так как ее можно обнаружить статическим испытанием. С этой целью ось звена устанавливают на два горизонтальных ножа (опоры). Если центр масс расположен на оси вращения, то звено будет находиться в равновесии при любом положении, в противном случае оно покатится и будет двигаться, пока не достигнет устойчивого равновесия, при котором центр масс имеет самое низкое расположение. При изготовлении практически невозможно совместить центр масс детали с ее осью вращения, т.е. центр масс вращающейся детали будет смещен на некоторую величину от ее оси. Для статического уравновешивания детали необходимо в направлении, противоположном центру масс, установить корректирующую массу
Если будет выполнено условие (6.4), то сила инерции противовеса
Результирующая сила инерции при этом условии будет равна нулю. Условие (6.4) достигается обычно путем проб. Иногда установку противовеса заменяют удалением (например, высверливанием) массы
Рис. 6.1. Статическая балансировка ротора: 1 – ротор, 2 – ножи (опора), 3 – уровень После установки корректирующей массы Статического уравновешивания достаточно только для звеньев, имеющих малую осевую протяженность (например, шкивы, маховики, фланцы, зубчатые колеса, дисковые фрезы, авиационные винты, велосипедные колеса и т. п.). Для звеньев другой формы (например, для валов) должны быть выполнены оба условия уравновешенности звена (6.1) и (6.2) – главный вектор и главный момент сил инерции в этом случае равны нулю и полностью устраняется давление на стойку от сил инерции. Полное уравновешивание вращающихся звеньев Пусть необходимо выполнить полное уравновешивание твердого тела, вращающегося в опорах (рис. 6.2). Покажем, что любую вращающуюся деталь можно уравновесить с помощью установки двух корректирующих масс в двух произвольно выбранных плоскостях коррекции I и II. При вращении твердого тела на его любую элементарную массу, например
где Заменим эту центробежную силу инерции
Рис. 6.2. Полное уравновешивание вращающегося тела
Найдем силы инерции от всех элементарных масс, распределенных вдоль оси вращения. Для каждой силы выполним процедуру приведения к плоскости I и II по формулам (6.6), найдем суммарные силы инерции, действующие на I и II плоскостях.
Тогда корректирующие массы
Углы расположения этих масс находятся из уравнений:
Установив соответствующие корректирующие массы в двух плоскостях коррекции, мы полностью сбалансируем деталь. Экспериментальное определение неуравновешенности вращающегося звена и ее устранение называется балансировкой. Она производится на балансировочных станках. Уравновешивание жесткого ротора На рис. 6.3 изображена принципиальная схема балансировочного станка Б.В. Шитикова.
Рис. 6.3. Балансировочный станок: 1 – рама; 2 – неподвижная опора; 3 – подвижная опора; 4 – ротор; 5 – измерительное устройство;
Принцип работы балансировочного станка основан на измерении амплитуды колебаний механической системы с одной степенью свободы при вынужденных колебаниях на резонансе. Из теории колебаний известно, что амплитуда вынужденных колебаний механической системы с одной степенью свободы на резонансе прямо пропорциональна вынуждающей силе. Амплитуда колебаний A и гармоническая вынуждающая сила
где Предположим, что ротор имеет некоторую точечную неуравновешенную массу
здесь Вертикальная составляющая гармонической силы инерции Если с помощью измерительного устройства 5 измерить амплитуду вынужденных колебаний рамы с ротором на резонансе, тогда из уравнения (6.8) можно определить После этого, чтобы сбалансировать ротор, нужно в плоскости коррекции установить корректирующую массу · выполнялось равенство
· корректирующая сила инерции была направлена противоположно силе инерции неуравновешенной массы. Для того чтобы устранить дисбаланс, приведенный ко второй плоскости коррекции, нужно переставить ротор, поменяв опоры местами, и повторить вышеизложенные операции. Таким образом, для практического решения задачи балансировки ротора в опытах требуется для каждой плоскости коррекции определить: модуль дисбаланса; направление силы инерции неуравновешенной массы. Динамическое уравновешивание жестких роторов на балансировочном станке выполняется следующим образом. 1. Устанавливаем в станок ротор, подлежащий балансировке. 2. Выбираем плоскости коррекции. Это плоскости I и II. В каждой плоскости коррекции проводим ось ОХ. 3. Включаем станок и раскручиваем ротор так, чтобы его частота вращения лежала в зарезонансной области. 4. Отключаем станок и переводим ротор в режим выбега. 5. При прохождении резонанса с помощью измерительного устройства 5 измеряем амплитуду колебаний 6. Неизвестная неуравновешенная центробежная сила инерции на резонансе будет расположена в поперечном сечении ротора под некоторым углом
Рис. 6.4. Расположение сил инерции в плоскости 7. Установим на расстоянии
8. После закрепления дополнительной массы включаем станок и раскручиваем ротор так, чтобы его частота вращения лежала в зарезонансной области. 9. Отключаем станок и переводим ротор в режим выбега. 10. При прохождении резонанса с помощью измерительного устройства 5 измеряем амплитуду колебаний В соответствии с (6.8) во втором опыте определится 11. Переустанавливаем массу 12. После закрепления дополнительной массы включаем станок, раскручиваем ротор так, чтобы его частота вращения лежала в зарезонансной области, отключаем станок и переводим ротор в режим выбега. 13. При прохождении резонанса с помощью измерительного устройства 5 измеряем амплитуду колебаний 14. Находим модули сил В результате этих действий получим параллелограмм, который изображен на рис. 6.4, г. Для параллелограмма со сторонами
или
откуда
или
С учетом (6.8) получим
здесь Для коэффициента пропорциональности справедливо
15. Определяем дисбаланс ротора, учитывая, что согласно (6.8)
а также
откуда следует
16. Определяем параметры коррекции из условия
1. Задавая, например, радиус 2. Находим угол, на который нужно отклонить от оси ОХ радиус
откуда
где 3. После подстановки в (6.14) амплитуд колебаний в соответствии
Последнее уравнение дает два значения угла. Чтобы узнать, который из углов является истинным, необходимо провести дополнительный эксперимент. Для этого устанавливаем на деталь корректирующую массу под любым углом из найденных по формуле (6.15). Включаем станок и после разгона ротора переводим его в режим выбега. Во время резонанса измеряем амплитуду. Если амплитуда стала значительно меньше, чем была при первом испытании, то угол выбран правильно. Если амплитуда осталась большой, то угол был выбран неверно и корректирующую массу надо переустановить, а эксперимент повторить. На этом балансировка детали во второй корректирующей плоскости закончена. Переустанавливаем ротор в станке и проводим его балансировку в первой плоскости коррекции в соответствии с вышеописанным алгоритмом. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомиться с конструкцией и принципом действия балансировочной машины резонансного типа. Установить регулировочными винтами маятниковую раму машины в горизонтальное положение и диски корректирующих плоскостей в нулевое положение. 2. Вычертить схему балансировочной машины. Записать значения дополнительной массы и радиус ее установки. 3. Провести балансировку ротора в соответствии с описанным выше алгоритмом. Амплитуды в каждом опыте измерять минимум три раза. В расчетах использовать средние значения амплитуд. 4. Вычислить дисбаланс. 5. Определить угол установки корректирующей массы. 6. Задав массу, найти радиус установки корректирующего груза. 7. Установить массу в прорези диска машины согласно расчетам. 8. Провести опыт для определения снижения амплитуды и в случае его увеличения переустановить противовес в диаметрально противоположное положение. 9. Закрепить окончательно противовес в прорези диска машины под углом 10. Оформить отчет. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Отчего машины шумят и вибрируют? 2. Как борются с вибрациями в машинах?
|

 Трение представляет собой сопротивление относительному перемещению двух тел, возникающее в касательном направлении в зоне их соприкосновения. Сила сопротивления является силой трения.
Трение представляет собой сопротивление относительному перемещению двух тел, возникающее в касательном направлении в зоне их соприкосновения. Сила сопротивления является силой трения.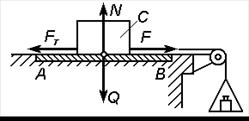
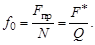
 Полная реакция связи R будет отклонена от нормали к поверхности на некоторый угол. При изменении силы трения F т от нуля до F пp сила R будет меняться от N до R пp, а ее угол с нормалью будет расти от нуля до некоторого предельного значения j0 (рис. 5.2). Наибольший угол j0, который полная реакция шероховатой связи образует с нормалью к поверхности, называется углом трения
Полная реакция связи R будет отклонена от нормали к поверхности на некоторый угол. При изменении силы трения F т от нуля до F пp сила R будет меняться от N до R пp, а ее угол с нормалью будет расти от нуля до некоторого предельного значения j0 (рис. 5.2). Наибольший угол j0, который полная реакция шероховатой связи образует с нормалью к поверхности, называется углом трения


 Передаточное отношение i винтовой пары равно отношению окружной vt и осевой va скоростей гайки (винта) (рис. 5.6).
Передаточное отношение i винтовой пары равно отношению окружной vt и осевой va скоростей гайки (винта) (рис. 5.6). или
или 
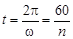



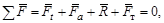


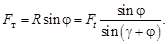
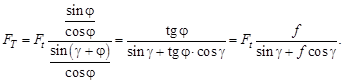

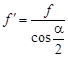 и
и  .
.

 Экспериментальная установка (рис. 5.12) состоит из плиты 1, в вертикальной стенке которой выполнено отверстие для установки винтовой пары (болта 2 и гайки 3). К плите 1 прикреплена скоба 4, перемещение которой фиксируется индикатором часового типа 5.
Экспериментальная установка (рис. 5.12) состоит из плиты 1, в вертикальной стенке которой выполнено отверстие для установки винтовой пары (болта 2 и гайки 3). К плите 1 прикреплена скоба 4, перемещение которой фиксируется индикатором часового типа 5.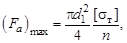


 и
и  . Занести их в табл. 5.2.
. Занести их в табл. 5.2.
 и главный момент сил инерции
и главный момент сил инерции 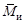 были равны нулю в любой момент движения:
были равны нулю в любой момент движения: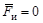 , (6.1)
, (6.1) . (6.2)
. (6.2)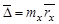 . (6.3)
. (6.3)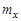 – масса звена;
– масса звена; 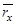 – расстояние от центра тяжести до оси вращения.
– расстояние от центра тяжести до оси вращения. . (6.4)
. (6.4)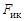 окажется равной и противоположной силе инерции
окажется равной и противоположной силе инерции 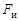 неуравновешенного звена:
неуравновешенного звена: . (6.5)
. (6.5) . Центр удаляемой массы и центр масс звена располагаются в этом случае по одну сторону от оси вращения.
. Центр удаляемой массы и центр масс звена располагаются в этом случае по одну сторону от оси вращения.
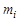 , действует центробежная сила инерции
, действует центробежная сила инерции 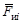 .
.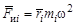 ,
,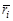 – радиус вектор элементарной массы
– радиус вектор элементарной массы  ,
,  . (6.6)
. (6.6)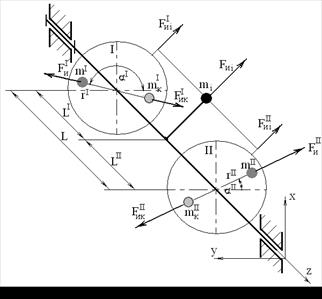
 ,
,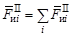 .
. и
и  для плоскости I и II соответственно могут быть выбраны из условий равенства модулей дисбалансов в двух плоскостях:
для плоскости I и II соответственно могут быть выбраны из условий равенства модулей дисбалансов в двух плоскостях: ,
,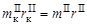 . (6.7)
. (6.7)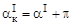 ,
, .
.
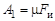 , (6.8)
, (6.8)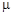 – коэффициент пропорциональности, зависящий от параметров станка.
– коэффициент пропорциональности, зависящий от параметров станка.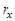 от оси вращения. При вращении ротора 4 с угловой скоростью
от оси вращения. При вращении ротора 4 с угловой скоростью 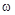 на его неуравновешенную массу
на его неуравновешенную массу  , которая может быть разложена на вертикальную
, которая может быть разложена на вертикальную 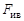 и горизонтальную
и горизонтальную  составляющие:
составляющие: ,
, ,
,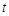 – время.
– время. и характеристику несбалансированности ротора – дисбаланс
и характеристику несбалансированности ротора – дисбаланс  .
. так, чтобы:
так, чтобы: ; (6.9)
; (6.9)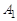 . В соответствии с (6.8) определится
. В соответствии с (6.8) определится 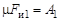 .
.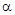 к оси ОХ (рис. 6.4, а).
к оси ОХ (рис. 6.4, а).
 от оси вращения на плоскости коррекции II массу
от оси вращения на плоскости коррекции II массу  в произвольно выбранном месте (например, на оси ОХ). При вращении ротора от этой дополнительной массы возникнет сила инерции
в произвольно выбранном месте (например, на оси ОХ). При вращении ротора от этой дополнительной массы возникнет сила инерции 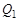 , для которой справедливо равенство
, для которой справедливо равенство . (6.10)
. (6.10)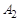 .
.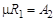 , где
, где 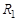 – векторная сумма сил инерции
– векторная сумма сил инерции 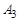 . В соответствии с (6.8) в третьем опыте определится
. В соответствии с (6.8) в третьем опыте определится 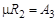 , где
, где  – модуль векторной суммы сил инерции
– модуль векторной суммы сил инерции  и
и  и диагоналями
и диагоналями 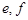 справедливы соотношения:
справедливы соотношения: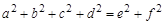
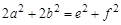 ,
, ,
,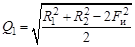 .
. , (6.11)
, (6.11)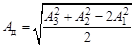 .
. . (6.12)
. (6.12) ,
,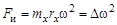 ,
,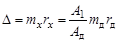 .
. (рис. 6.4, г). В соответствии с теоремой косинусов имеем:
(рис. 6.4, г). В соответствии с теоремой косинусов имеем: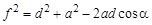 ,
, , (6.14)
, (6.14)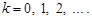
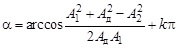 . (6.15)
. (6.15)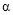 , при котором амплитуда колебаний рамы минимальна.
, при котором амплитуда колебаний рамы минимальна.


