Утверждено Редакционно-издательским советом университета в качестве учебно-методического пособия 2 страница
Т а б л и ц а 1.3 Классификация звеньев механизма
Т а б л и ц а 1.4 Классификация кинематических пар механизма
Т а б л и ц а 1.5 Классификация структурных групп механизма
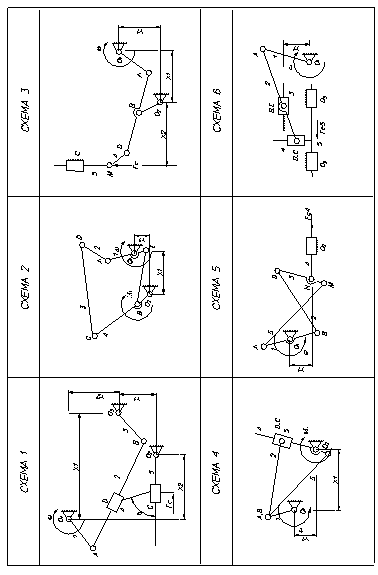
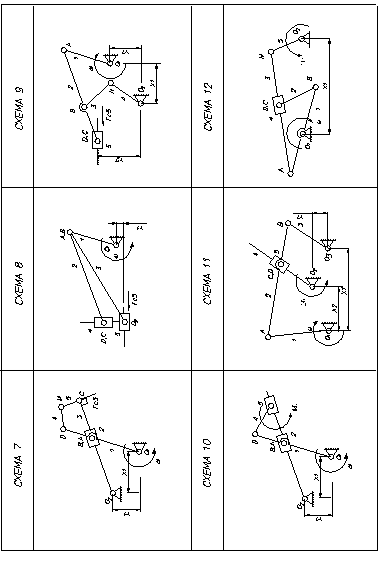
Порядок выполнения работы 1. Ознакомиться с моделью механизма, определить характер относительного движения звеньев. 2. Определить число звеньев и кинематических пар и вычертить структурную схему (эскиз) механизма (от руки в произвольном масштабе) при таком положении входного звена, чтобы другие звенья были видны достаточно наглядно и не было их наложения 3. Классифицировать звенья механизма и кинематические пары. Результаты представить в виде таблицы. 4. Определить степень подвижности механизма. 5. При наличии пассивных связей и лишних степеней подвижности показать, в чем они заключаются, удалить те звенья и кинематические пары, которым они принадлежат. 6. Если в состав механизма входят высшие кинематические пары, то необходимо каждую из них заменить фиктивным звеном c двумя парами I класса и вычертить эскиз заменяющего механизма, определить степень подвижности заменяющего механизма. 7. Вычертить в масштабе кинематическую схему механизма. 8. Провести структурную классификацию механизма. В порядке контроля определить степень подвижности каждой группы Ассура, ее класс, порядок и вид. 9. Определить дополнительные структурные параметры, доказывающие, что исследуемая структура является механизмом. 10. Оформить титульный лист и отчет о выполненной работе в указанном выше порядке. 11. Сформулировать выводы по лабораторной работе.
Вопросы для самоконтроля 1. Что такое машина, механизм? 2. Что такое деталь, звено? 3. Для чего и как составляют структурные и кинематические схемы механизма? 4. Какие бывают типы и виды звеньев механизма? 5. Какие бывают виды кинематических пар? 6. Классификация кинематических пар. 7. Как определяется подвижность механизмов? 8. Что такое структурная группа? 9. Как классифицируются структурные группы? 10. Проведите замену высшей кинематической пары.
ЛАБОРАТОРНАЯ РАБОТА № 2 ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ ЦЕЛЬ РАБОТЫ 1. Изучение условия проворачиваемости звеньев рычажных механизмов. 2. Определение размеров звеньев механизма из табл. 2.1. 3. Построение кинематической схемы механизма согласно найденным длинам звеньев. 4. Определение крайних положений звеньев исследуемого механизма. ОСНОВНЫЕ СВЕДЕНИЯ Параметрическим синтезом механизма называется определение соотношений длин его звеньев, удовлетворяющих определенным условиям. Выясним, каковы эти соотношения у четырехзвенных механизмов. В зависимости от выбора в кинематической цепи входного звена и стойки получают различные механизмы с измененным характером относительного движения некоторых звеньев. Если в плоской структурной схеме шарнирного четырехзвенника, образованного плоской замкнутой кинематической цепью, стойкой будет звено 1, то получим кривошипно-коромысловый механизм (рис. 2.1, а). Если закрепить неподвижно наименьшее звено 2 и сделать входным звено 3, то образуется другой вариант этого механизма – двухкривошипный (рис. 2.2, б). Такой прием получения вариантов механизма и его компоновок посредством замены функций одного звена функциями другого называется инверсией. Использование метода инверсии возможно при соотношениях длин звеньев, определяемых условием существования кривошипа в шарнирном четырехзвеннике. Инверсией кривошипно-ползунного механизма (рис. 2.2, а) при превращении ползуна 3 в стойку, а звена 2 – во входное звено получаем механизм с поступательно движущимся звеном 3 (рис. 2.2, б). Кривошипно-ползунный механизм превращается в кривошипно-кулисный,
а б Рис. 2.1. Инверсия механизма шарнирного четырехзвенника
если за стойку принять звено 1, а за входное звено – звено 2 (звено 0 станет кулисой, рис. 2.2, в). Таким образом, с помощью инверсии можно получить механизмы, обеспечивающие различный характер движения выходного звена. Связь между размерами звеньев четырехзвенных механизмов и их движением может быть представлена математически в виде некоторых неравенств. Рассмотрим случай, когда за выходное звено может быть принято любое из четырех звеньев механизма, но при определенном соотношении их размеров. Пусть l 1– самое короткое звено механизма (рис. 2.3), а l 2 или l 3– самое длинное.
а б в Рис. 2.2. Инверсия кривошипно-ползунного механизма
Рис. 2.3. Условие проворачиваемости звеньев
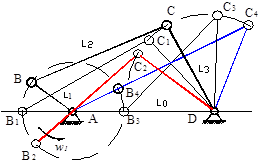
Для того чтобы при вращении кривошипа 1 точка В попала в положение В 1, необходимо соблюдать неравенство l 1 + l 0 < l 2 + l 3. (2.1) Из свойств треугольника следует также, что при l 2 > l 3 l 1 + l 0 > l 2 – l 3. (2.2) Для прохождения точки В через положение В 3 необходимо соблюдать неравенство l 0 – l 1 < l 2 + l 3, (2.3) а при l 2 > l 3 следует, что l 0 – l 1 > l 2 – l 3. (2.4) Неравенство (2.1) исключает неравенство (2.3), неравенство (2.4) исключает неравенство (2.2). Тогда для случая l 2 > l 3получим систему неравенств l 1 + l 0 < l 2 + l 3, l 1 + l 2 < l 0 + l 3. Так как l 1– наименьшее звено, то при наибольшем звене l 2 неравенство l 1 + l 2 < l 0 + l 3 (2.5) обеспечивает выполнение остальных условий. При наибольшем звене l 3 условие прохождения точки В через В 1 и В 3 выражается неравенством l 1 + l 3 < l 2 + l 0 . (2.6) Неравенства (2.5) и (2.6) позволяют сформулировать условие проворачиваемости звеньев – правило Ф. Грасгофа (1826–1893 гг.). Самое короткое звено шарнирного механизма (рис. 2.4) будет кривошипом, если сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев. Из этого следует, что: · механизм будет двухкоромысловым (рис. 2.4, а), если размеры его звеньев не удовлетворяют указанному правилу; · кривошипно-коромысловым (рис. 2.4, б), если размеры его удовлетворяют правилу и кривошип – самое короткое звено; · двухкривошипным (рис. 2.4, в), если размеры его звеньев удовлетворяют правилу и за стойку принято самое короткое звено.
а б в Рис. 2.4. Модификации шарнирного четырехзвенника
Условия проворачиваемости справедливы и для четырехзвенных механизмов, имеющих поступательную кинематическую пару. Рассмотрим преобразование вращательной пары в поступательную пару. Так как центр вращательной пары С движется по окружности радиуса D ¢ C (рис. 2.5, а), то кинематика звеньев 1 и 2 не изменяется, если звено 3 механизма заменить ползуном, двигающимся по круговой направляющей того же радиуса. При увеличении длины l 3звена 3 направляющая выпрямится и при Если при
Рис. 2.5. Модификации шарнирного четырехзвенника с поступательными
Увеличивая размеры элементов кинематической пары В и не изменяя длину звена 1 – l 1, получают механизмы других типов, но обладающих такой же проворачиваемостью звеньев и кинематикой, как и в шарнирном четырехзвеннике. В этих механизмах звено 1 превращается в эксцентрик с эксцентриситетом (смещением) е = l 1. Обычно такие механизмы конструктивно удобно выполнять при l 1, соизмеримых с диаметрами шарниров кинематических пар. Крайние, мертвые, положения механизма определяют аналитически или графически. Если начальное и выходное звенья совершают вращательные движения, то крайние положения в механизме отсутствуют. К таким механизмам относят, например, зубчатые, двухкривошипные механизмы. Покажем определение крайних положений звеньев следующих механизмов. Пусть выходное звено шарнирного четырехзвенника (рис. 2.6) совершает колебательное (возвратно-вращательное) движение. Тогда крайними положениями коромысла будут положения, когда кривошип 1 и шатун 2 складываются в одну линию (положение 2, рис. 2.6, а), или вытягиваются (положение 4, рис. 2.6, б). Соответствующие крайним положениям коромысла положения кривошипа определяются углами, φ1н, φ1к. Рабочим ходом таких механизмов, является перемещение коромысла 3 навстречу моменту сопротивления М с, поэтому углы φ1н и φ1к определяют соответственно начало и конец рабочего хода коромысла 3. Отсчет искомых углов проводится от оси ОХ, против движения часовой стрелки до звена 1, положение которого определяется.
а б Рис. 2.6. Определение крайних положений шарнирного четырехзвен- а – начальное положение коромысла; б – конечное положение
В рассматриваемом примере угол φ1н = φ + 180°, где Звено 3 является выходным звеном кривошипно-ползунного механизма (рис. 2.7). Крайние положения ползуна 3 определяются положениями кривошипа 1 и шатуна 2 в момент их складывания (положение 2) и распрямления (положение 4). Поскольку направление рабочего хода противоположно направлению основной силовой характеристики механизма – силы сопротивления F c, крайнее левое положение ползуна 3 будет началом рабочего хода, а крайнее правое положение звена 3 – соответственно концом рабочего хода. Обратное движение ползуна 3, когда F c = 0, называется холостым ходом.
Рис. 2.7. Определение крайних положений
Положение кривошипа в момент начала движения ползуна 3 характеризуется углом φ1н = β + 180°, где Для кулисного механизма с качающейся кулисой (рис. 2.8) крайними являются положения, когда кривошип 1 и кулиса 3 взаимно перпендикулярны или, что то же самое, когда кулиса является касательной к траектории движения вершины В кривошипа. Расположим кулисный механизм так, чтобы одна из его координатных осей проходила по линии, соединяющей центры кинематических пар, которыми механизм присоединяется к стойкам, а вторая –
Рис. 2.8. Определение крайних положений через стойку кривошипа. Установим направление движения кривошипа по часовой стрелке, а направление М с – против. Если углы кривошипа φ1н, φ1к определяют начальное и конечное положения кулисы, то их значения вычисляются по Для построения плана положений i механизма методом засечек необходимо определить масштабный коэффициент длин звеньев механизма μl = l к/ (AB) (м/мм), где l к – истинная длина кривошипа, а (АВ) – выбранный чертежный размер кривошипа (50…70 мм). Выбрав место расположения стойки А начального звена, строим траекторию (окружность) движения подвижной вершины кривошипа В радиусом R 1 = (АВ). Положения i выходного звена 3, кривошипно-коромыслового механизма (рис. 2.6), соответствующие выбранным положениям кривошипа (АВi), определены точками пересечения окружностей R 2 = (Вi Сi) Откладывая (СK) = lСK / μ l, строим траекторию (линию) движения ползуна 3, кривошипно-ползунного механизма (рис. 2.7). Выбрав положение i вращательной пары Вi на траектории движения вершины кривошипа, проводим окружность радиусом R 2 = (Вi Сi), где (Вi Сi) = lВС / μ l. Пересечение траектории движения ползуна с окружностью R 2 позволяет определить положение ползуна 3, соответствующее положению i кривошипа 1. Прямые (DСi), проведенные через стойку D, и положения вершины Вi кривошипа 1 составляют план положений i кривошипно-кулисного механизма (рис. 2.8). Порядок выполнения работы 1. Ознакомиться с моделью механизма, определить характер относительного движения звеньев. 2. Определить степень подвижности механизма. 3. Определить размеры звеньев из условия проворачиваемости звеньев. 4. Вычертить в масштабе кинематическую схему механизма. 5. Вычислить углы при кривошипе, соответствующие крайним положениям выходного звена. 5. Рассмотреть другие варианты механизма. 6. Оформить титульный лист и отчет о выполненной работе. 7. Сформулировать выводы по лабораторной работе.
Вопросы для самоконтроля 1. Что такое инверсия механизмов? 2. Сформулируйте условие проворачиваемости звеньев, правило Ф. Грасгофа. 3. Дайте пояснения к методу построения положений механизма. 4. Какие положения звеньев механизма называют крайними? 5. Как определяются углы кривошипа в крайних положениях?
Т а б л и ц а 2.1 Задание на лабораторную работу
О к о н ч а н и е т а б л. 2.1
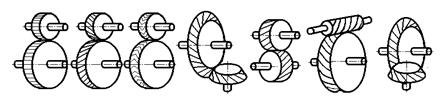
Лабораторная работа № 3 Кинематический анализ Цель работы 1. Ознакомление с различными видами зубчатых механизмов и составление их кинематических схем. 2. Проведение кинематического анализа этих механизмов аналитическим, графическим и экспериментальным методами. Основные сведения Зубчатые передачи относятся к механическим и предназначены для передачи вращательного движения от ведущего вала к ведомому с преобразованием параметров этого движения: угловых скоростей и крутящих моментов. Трехзвенный зубчатый механизм состоит из двух подвижных звеньев – зубчатых колес, находящихся в зацеплении и образующих кинематическую пару II класса, и входящих во вращательные кинематические пары I класса с третьим неподвижным звеном – стойкой. Основным классификационным признаком трехзвенных зубчатых механизмов является взаимное расположение осей вращения колес. Различают механизмы: C с параллельными осями – цилиндрические прямозубые (рис. 3.1, а), косозубые (рис. 3.1, б), шевронные (рис. 3.1, в), реечные, с внешним
а б в г д е з Рис. 3.1. Трехзвенные зубчатые механизмы C с пересекающимися осями – конические (рис. 3.1, г) прямозубые, косозубые, тангенциальные); C с перекрещивающимися осями – винтовые (рис. 3.1, д), червячные (рис. 3.1, е), гипоидные (рис. 3. 1, з). Трехзвенные зубчатые механизмы в различных сочетаниях могут быть скомбинированы в многозвенных зубчатых механизмах. Например рядовой механизм с промежуточными колесами (рис. 3.2), в котором окружные скорости Vi всех колес одинаковы, а следовательно, промежуточные колеса 2, 3 и 4, изменяя направление вращения, не влияют на величину выходной угловой скорости ω5.
Рис. 3.2. Рядовой зубчатый механизм
Рис. 3.3. Рядовой ступенчатый
Могут быть образованы рядовые ступенчатые зубчатые механизмы (рис. 3.3), в которых промежуточные колеса парами устанавливаются на общей оси и влияют на изменение выходной угловой скорости ω4. Существуют более сложные зубчатые механизмы с подвижными осями колес: планетарные и дифференциальные (рис. 3.4), а также их комбинации с рассмотренными ранее типами механизмов. Структура зубчатых механизмов Простой трехзвенный плоский механизм (рис. 3.5) состоит из двух цилиндрических зубчатых колес 1 и 2, закрепленных шарнирно в стойке 0 (корпусе). Такой механизм имеет два подвижных звена (колеса), две кинематические пары I класса p 1 (цилиндрические шарниры) и одну кинематическую пару II класса p 2 (зацепление зубьев). В соответствии с формулой Чебышева степень подвижности такого механизма
Иначе обстоит дело в зубчатых механизмах имеющих подвижные оси колес, – дифференциальных механизмах. Дифференциальный механизм Давида (рис. 3.4) содержит стойку 0, три подвижных зубчатых колеса: солнечную шестерню 1, центральное колесо с внутренними зубьями 2 и сателлит 3, ось которого, закрепленная в водиле 4, движется по круговой орбите вокруг центральной оси. Число подвижных звеньев в таком механизме n = 4, кинематических пар I класса p 1 = 4 и два зубчатых зацепления каждые из которых образуют кинематическую пару II класса (p 2 = 2). После подстановки значения n, p 1, p 2 в формулу Чебышева имеем
Это значит, что для получения заданного закона вращения, например колеса 2, необходимо совместно подать вращение на шестерню 1 и водило 4. Однако, закрепив центральное колесо 2 неподвижно на стойке, можно получить другой механизм с подвижными осями – планетарный. Для него число подвижных звеньев уменьшится на единицу (n = 3), кинематических пар первого класса также станет на одну меньше
Сложные механизмы, состоящие из рассмотренных выше видов механизмов, могут иметь степень подвижности и больше двух. Кинематика зубчатых механизмов Основной задачей кинематического анализа зубчатых механизмов является определение их передаточных отношений. Изучение кинематики начнем с простейших типов зубчатых механизмов. На рис. 3.5 схематично показана цилиндрическая зубчатая передача с внешним зацеплением. Скорости точек начальных окружностей колес, перекатывающихся друг по другу без скольжения, одинаковы и равны V. Следовательно, угловые скорости вращения колес будут обратно пропорциональны их диаметрам:
Общее передаточное отношение многоступенчатого механизма будет определяться произведением передаточных отношений ступеней. Знак передаточного отношения i для четного числа сомножителей – положительный (вращение первого и последнего колес в одну сторону), а для нечетного – отрицательный. В рядовых зубчатых механизмах (см. рис. 3.2), в которых промежуточные колеса входят в два зубчатых зацепления, передаточное отношение будет Для исследования кинематики зубчатых механизмов с подвижными осями колес (планетарных и дифференциальных) воспользуемся методом мысленного останова водила (метод Виллиса). Суть этого метода заключается в том, что весь механизм мысленно начинают вращать вокруг центральной оси О 1 – О 2 с угловой скоростью, равной по величине и противоположной угловой скорости водила. В результате этого сложения вращений водило останавливается в пространстве. Вновь полученный обращенный механизм превращается в обычный ступенчатый (или рядовой) с неподвижными осями колес. Определить передаточное отношение обращенного механизма можно рассмотренным выше способом. Перейдем к порядку применения метода Виллиса для кинематического расчета дифференциального механизма (рис. 3.6). На вход механизма поданы две угловые скорости: w1 – угловая скорость шестерни рядового механизма; w Н – угловая скорость вала водила дифференциального механизма. Для определения угловой скорости центрального колеса дифференциала 2¢ умножим w1 на передаточное отношение i 12 = – z 2/ z 1 w2¢= w1(–) z 2/ z 1. Теперь в соответствии с методом Виллиса мысленно преобразуем механизм, сообщив вращение дифференциальному механизму вокруг центральной неподвижной оси с угловой скоростью водила w Н, но в обратном направлении. Вращение водила и мысленное обратное движение
Рис. 3.6. Графические методы определения передаточного отношения: а – кинематическая схема замкнутого дифференциала; б – план скоростей точек звеньев замкнутого дифференциала;
складываются и в сумме дают нуль, т. е. водило мысленно останавливается, а все остальные колеса получают дополнительную отрицательную скорость водила w Н. При этом все оси колес мысленно преобразованного механизма становятся неподвижными, т. е. это ступенчатый механизм. Движение в этом механизме будет передаваться от центрального колеса 2 ¢, мысленно вращаемого с угловой скоростью w2¢ – w Н, через блок сателлитов 3 - 3 ¢ с неподвижной осью, к солнечной шестерне 4, скорость вращения которой будет w4 – w Н. Для преобразованного ступенчатого механизма передаточное отношение
Помножим правую и левую часть на (ω4 – ω Н), получим
Учитывая, что
|
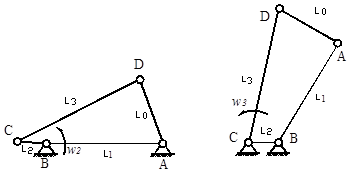
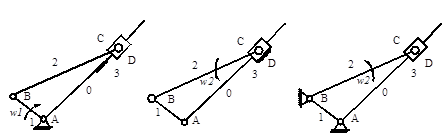
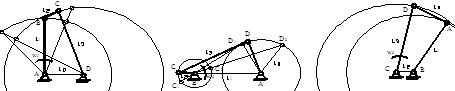
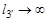станет прямолинейной. В этом случае механизм превратится 
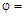
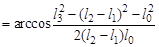, а 
.
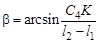. Угол при кривошипе в конце рабочего хода определяется из 
.
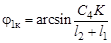, а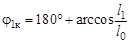 
.
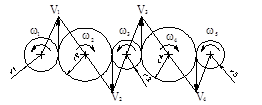
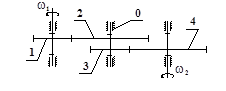
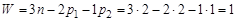, т. е. вращение ведущего звена 1 (шестерни) передается ведомому звену 2 (колесу) и однозначно определяет его положение.
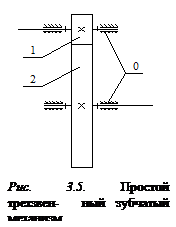Аналогично выполняется расчет степени подвижности и для многозвенных рядовых и ступенчатых механизмов. Причем, несмотря на увеличение числа звеньев и кинематических пар, степень подвижности зубчатых механизмов с неподвижными осями колес остается равной единице.
.
.
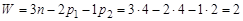. Отсюда передаточное отношение i, равное отношению угловой скорости ведущего колеса к угловой скорости ведомого, будет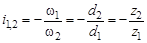 
. Последнее соотношение чисел зубьев колес получено вследствие того, что 
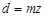, а условный знак (–) указывает на то, что вращение колес с внешним зацеплением, происходящее в одной плоскости, является встречным. Максимальное значение передаточного отношения рассматриваемой передачи не рекомендуется принимать более шести из соображений компактности передачи: диаметр колеса будет существенно больше диаметра шестерни. Если все же необходимо получить большее передаточное отношение, целесообразно разбить передачу на две ступени (см. рис. 3.3). В таком ступенчатом зубчатом механизме передаточное отношение (с учетом того, что 
) равно
.
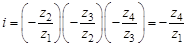, т. е. промежуточные колеса влияют не на величину передаточного отношения, а только на его знак. Применяют такие механизмы для обеспечения требуемого межцентрового расстояния или изменения направления вращения.
.
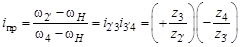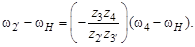
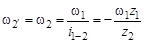, получаем
