Утверждено Редакционно-издательским советом университета в качестве учебно-методического пособия 4 страница
Угол профиля
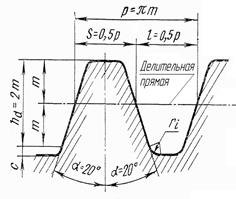
Рис. 4.5. Исходный контур
Расчетные формулы приведены в табл. 4.2.
Т а б л и ц а 4.2 Формулы для расчета геометрических параметров некоррегированных прямозубых цилиндрических колес внешнего и внутреннего зацепления
Коррегирование зубчатых колес Коррегированием зубчатых колес называют преднамеренное изменение стандартных пропорций зубьев, заданных исходным контуром. Чаще всего коррегирование производят, чтобы устранить подрезание зубьев (рис. 4.6, а), возникающее при нарезании колес с малым числом зубьев методом обкатки, и получать равную прочность у сопряженной пары – шестерни и колеса. Подрезание снижает прочность зубьев, сокращает продолжительность их зацепления и отрицательно влияет на плавность работы. Наименьшее число зубьев шестерни, свободное от подрезания, определяется из уравнения
где Цилиндрические колеса с числом зубьев меньше При изменении положения режущего инструмента относительно центра нарезаемого зубчатого колеса делительная окружность будет
Рис. 4.6. Смещение зуборезного инструмента при коррегировании катиться по делительной прямой 2, смещенной относительно средней линии на величину
Смещение средней линии рейки относительно делительной окружности в направлении от оси колеса называют положительным смещением, а в направлении к оси колеса – отрицательным смещением. Коэффициентом смещения Наибольшее распространение получили два способа коррегирования зубчатых колес – высотный и угловой. При высотном коррегировании шестерню изготовляют с положительным смещением исходного контура ( При угловом коррегировании сумма коэффициентов смещения не равна нулю ( Нарезание зубьев с высотным и угловым коррегированием производят стандартным зуборезным инструментом. В табл. 4.3 приведены формулы для расчета геометрических параметров коррегированных прямозубых цилиндрических колес внешнего зацепления.
Т а б л и ц а 4.3 Формулы для расчета геометрических параметров прямозубых
О к о н ч а н и е т а б л. 3.3
Оценка качества зацепления Коэффициенты смещения Качественные показатели взаимодействия двух сопряженных колес определяются характеристиками зацепления: коэффициентом перекрытия, удельным скольжением, правильностью зацепления – отсутствием интерференции. 1. Угол поворота зубчатого колеса от положения входа зуба в зацепление до выхода из зацепления называется углом перекрытия колеса. Для того чтобы выполнялись условия непрерывности взаимодействия зубьев, этот угол должен быть больше углового шага τ (рис. 4.7). Отношение угла перекрытия колеса к его угловому шагу называется коэффициентом торцевого перекрытия
или
Условие непрерывности взаимодействия зубьев выражается условиями Косвенным признаком повышения контактной прочности является увеличение угла зацепления Признаком повышения контактной прочности является также более высокая величина межосевого расстояния 2. Зубья зацепляющихся колес перекатываются и скользят друг
Так как в точке Е 1 – Воспользовавшись этими и промежуточными значениями
Т а б л и ц а 4.4 Значения величин удельного скольжения колес
Расчетные формулы для
где
Рис. 4.8. Скорости в зацеплении Максимальная износостойкость будет обеспечена в случае равенства максимальных ординат суммарных относительных скольжений шестерни и колеса; на этот критерий влияют величины смещений инструмента, позволяющие перемещать точки 3. Интерференция зубьев. Правильное зацепление зубчатых колес происходит лишь в том случае, если точка касания эвольвентных участков профиля взаимодействующих зубьев находится на линии зацепления. Поэтому должна быть устранена возможность касания этих профилей вне линии зацепления, что имеет место при кромочном касании, когда в работу вступают кромки зубьев (точки пересечения профилей с поверхностями вершин зубьев). Причинами кромочного касания являются недостаточный коэффициент перекрытия Интерференцией зубьев называется всякое неправильное касание профилей вне активного участка линии зацепления, т.е. явление, когда траектория кромки одного зуба пересекает профиль сопряженного зуба. При этом зуб одного колеса врезается в тело зуба другого колеса. Это имеет место при работе пары зубчатых колес и обычно называется внедрением профилей, как и при нарезании методом обкатки, когда происходит подрезание зубьев обрабатываемого колеса. При профильной интерференции (рис. 4.9, б)кромка зуба одного колеса внедряется в эвольвентную часть профиля зуба сопряженного колеса. При интерференции с переходной кривой (рис. 4.9, а)кромка зуба одного из зубчатых колес пересекает переходную поверхность другого зубчатого колеса. В случае нарезания зубьев методом обкатки интерференция кромки инструмента приводит к подрезанию зубьев колеса 2, а интерференция кромки зуба нарезаемого колеса с профилем инструмента приводит к срезу части профиля у головок зубьев колеса 1. Как указывалось выше, ограничениями для значений коэффициентов х является не только подрезание зубьев. Поэтому задача выбора коэффициентов смещения для зубчатого зацепления решается как задача оптимизации двух параметров
Рис. 4.9. Интерференция зубьев нанесены ограничения при выборе коэффициентов смещений: отсутствие подрезания и заострения зубьев, минимальные допустимые коэффициенты перекрытия и т. д. Эта область для определенного сочетания зубьев
Рис. 4.10. Блокирующий контур зацепления: 1 – граница интерференции на ножке зуба второго колеса; 2 – линия минимально допустимого коэффициента перекрытия; 3 – граница интерференции на ножке зуба первого колеса; 4 – граница заострения зуба на первом колесе; 5 и 6 – линии, определяющие подрезание эвольвентного профиля зацепляющихся зубьев. Для оптимального подбора коэффициентов смещений внутри блокирующего контура изображены линии, соответствующие наилучшим значениям качественных показателей зацепления: а – определяющие равную прочность зубьев обоих колес на изгиб при ведущем колесе 1; б – то же, при ведущем колесе 2; в – рекомендуемое значение коэффициента перекрытия Смещение инструмента при нарезании эвольвентных колес расширяет возможности эвольвентной зубчатой передачи, а именно: 1) предотвращает подрезание зубьев при 2) позволяет выравнять относительные скольжения и тем самым увеличить износостойкость, работоспособность поверхностей зубьев и уменьшить опасность заедания; 3) повышает изгибную прочность зубьев; 4) во всех случаях обеспечивает неподрезание зубьев шестерни, толщина зубьев по вершинам Методы изготовления зубчатых колес Эвольвентные профили зубчатых колес нарезают на металлорежущих станках методом копирования (рис. 4.11) и методом обкатки или огибания (рис. 4.12). 1. Метод копирования заключается в последовательном фрезеровании впадин между двумя зубьями. Профиль инструмента должен совпадать с профилем впадины между зубьями нарезаемого колеса (рис. 4.11, в). За один проход инструмент нарезает одну впадину между двумя соседними зубьями. Затем возвращается в исходное положение и заготовка поворачивается на угол Инструментом могут быть модульная (рис. 4.11, а), дисковая модульная фреза или пальцевая модульная фреза (рис. 4.11, б), строгальный или долбежный резец, протяжка, шлифовальный круг и др. Недостаток метода – большая номенклатура применяемого инструмента, так как для колес с разными числами зубьев нужен новый инструмент из-за изменения профиля впадины. Кроме этого, в процессе нарезания зубьев колес режущий инструмент изнашивается, изменяя профиль режущий части, а также при изготовлении самого инструмента неизбежны погрешности, которые переносятся на нарезаемое колесо, в результате чего точность зацепления снижается. Для внесения изменений в геометрию зубьев необходимо изготовить новый (специальный) инструмент, что трудоемко и неэкономично.
|

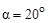 , нормальная величина радиального зазора равна
, нормальная величина радиального зазора равна 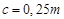 , а радиус закругления у корня зуба исходного контура составляет
, а радиус закругления у корня зуба исходного контура составляет 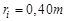 .
.
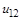
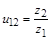
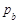 = m pcos a, где
= m pcos a, где 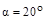
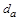
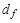
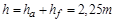
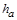
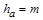
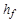
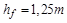
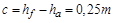
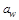
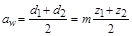
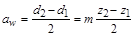
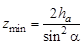 , (4.13)
, (4.13)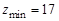 при
при 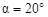 .
.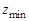 необходимо коррегировать. Коррегирование зубчатых колес производят смещением режущего инструмента реечного типа при нарезании зубьев. Принцип смещения инструмента при коррегировании показан на рис. 4.6. За нулевое положение принимают такое положение инструмента, при котором делительная окружность радиусом
необходимо коррегировать. Коррегирование зубчатых колес производят смещением режущего инструмента реечного типа при нарезании зубьев. Принцип смещения инструмента при коррегировании показан на рис. 4.6. За нулевое положение принимают такое положение инструмента, при котором делительная окружность радиусом  катится по средней линии 1 рейки исходного контура.
катится по средней линии 1 рейки исходного контура.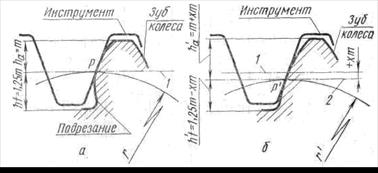
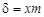 . (4.14)
. (4.14)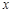 называют отношение величины радиального смещения делительной линии исходного контура к модулю,
называют отношение величины радиального смещения делительной линии исходного контура к модулю, 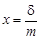 .
.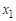 > 0), а колесо – с равным ему по абсолютной величине отрицательным смещением (
> 0), а колесо – с равным ему по абсолютной величине отрицательным смещением (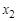 < 0). Сумма коэффициентов смещения равна нулю (
< 0). Сумма коэффициентов смещения равна нулю (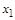
 , где z min = 17
, где z min = 17
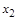
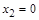 , при z 2 > z min
, при z 2 > z min
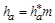
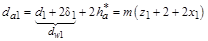
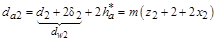
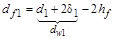 = m (z 1 – 2,5+ x 1)
= m (z 1 – 2,5+ x 1)
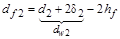 = m (z2 – 2,5+ x 1)
= m (z2 – 2,5+ x 1)
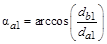
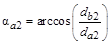
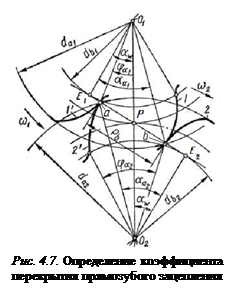 Коэффициент перекрытия. Для плавной и безударной работы пары зубчатых колес должно быть выполнено условие непрерывности смены зубьев. Это обеспечивается только в том случае, когда последующая пара зубьев начнет зацепление раньше, чем предыдущая его закончит. Непрерывность зацепления зубьев оценивается коэффициентом торцевого перекрытия
Коэффициент перекрытия. Для плавной и безударной работы пары зубчатых колес должно быть выполнено условие непрерывности смены зубьев. Это обеспечивается только в том случае, когда последующая пара зубьев начнет зацепление раньше, чем предыдущая его закончит. Непрерывность зацепления зубьев оценивается коэффициентом торцевого перекрытия 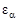 .
.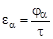 , где τ – угловой шаг,
, где τ – угловой шаг, 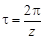 ;
;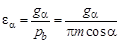
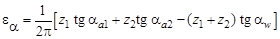 . (4.15)
. (4.15)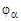 >
> 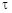 и
и 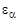 >1. В зависимости от технологического процесса обработки зубчатых профилей на основе опытных данных наименьшие величины коэффициентов перекрытия
>1. В зависимости от технологического процесса обработки зубчатых профилей на основе опытных данных наименьшие величины коэффициентов перекрытия 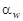 . Максимально возможной контактной прочности соответствуют
. Максимально возможной контактной прочности соответствуют 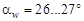 . Более высокие
. Более высокие 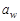 по сравнении с делительным межосевым расстоянием
по сравнении с делительным межосевым расстоянием 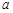 (в нулевой передаче они совпадают).
(в нулевой передаче они совпадают).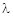 – отношение скорости скольжения
– отношение скорости скольжения 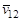 в точке контакта K к тангенциальной составляющей этой скорости
в точке контакта K к тангенциальной составляющей этой скорости 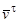 (рис. 4.8, а). Скорость скольжения определяется как разность тангенциальных составляющих абсолютных скоростей
(рис. 4.8, а). Скорость скольжения определяется как разность тангенциальных составляющих абсолютных скоростей 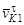 и
и 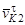 , а удельное скольжение для первого и второго колеса будет соответственно
, а удельное скольжение для первого и второго колеса будет соответственно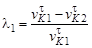 и
и 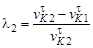 . (4.16)
. (4.16)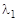 = –
= – 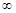 и
и 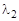 = 1; в точке Е 2 –
= 1; в точке Е 2 –  , мм
, мм
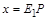
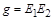
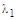
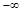
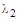
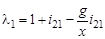 и
и 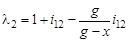 , (4.17)
, (4.17)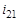 – передаточное отношение от колеса к шестерне;
– передаточное отношение от колеса к шестерне; 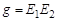 – длина линии зацепления (в мм), берется из построения с учетом масштаба;
– длина линии зацепления (в мм), берется из построения с учетом масштаба; 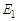 до текущей точки на линии зацепления,
до текущей точки на линии зацепления, 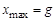 (рис. 4.8, б). Из опыта эксплуатации следует, что удельное скольжение не должно быть больше
(рис. 4.8, б). Из опыта эксплуатации следует, что удельное скольжение не должно быть больше 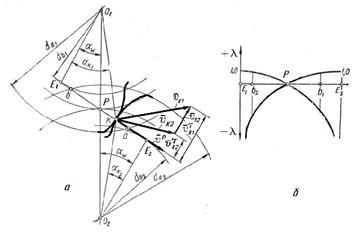
 ,на линии зацепления за счет изменения диаметров вершин.
,на линии зацепления за счет изменения диаметров вершин.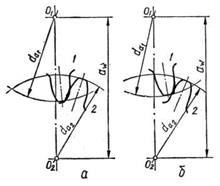
 и
и 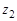 называется блокирующим контуром. Граничные линии блокирующего контура относятся к предельным значениям параметров
называется блокирующим контуром. Граничные линии блокирующего контура относятся к предельным значениям параметров
 и коэффициент перекрытия
и коэффициент перекрытия  .
.


