Утверждено Редакционно-издательским советом университета в качестве учебно-методического пособия 1 страница
Новосибирск УДК 621.01 (075.8) Т 338
Коллектив авторов: В.П. Гилета, Н.А. Чусовитин, Ю.В. Ванаг, Б.В. Юдин,
Рецензенты: канд. техн. наук, доц. А.Г. Козлов, канд. техн. наук, доц. А.А. Рыков
Работа подготовлена на кафедре прикладной механики
Т 338 Теория механизмов и машин: учебно-метод. пособие / коллектив авторов. – Новосибирск: Изд-во НГТУ, 2008. – 96 с. ISBN 978-5-7782-0971-8
Приведенные материалы систематизированы, содержат теоретическое обоснование, описание лабораторных установок, порядок выполнения и оформления работ, а также контрольные вопросы. Практикум поможет студентам в изучении важнейших разделов ТММ и при выполнении расчетно-графических и курсовых работ. Может быть рекомендован студентам МТФ, ФЛА, ЭМФ и ИДО
УДК 621.01 (075.8)
ISBN 978-5-7782-0971-8 Ó Коллектив авторов, 2008
Введение Курс «Теория механизмов и машин» является одной из дисциплин, обеспечивающих общетехническую подготовку студентов механических специальностей. Лабораторные работы по курсу закрепляют теоретические знания и прививают практические навыки проведения исследовательских работ и помогают студентам лучше понять суть физических процессов и явлений, происходящих в машинах. Цель лабораторных работ – научить студентов применять основные методы исследования к моделям механизмов, проводить измерения и испытания машин и механизмов, оформлять техническую документацию в виде отчета, обрабатывать результаты исследования, анализировать получаемые результаты и делать по ним выводы и заключения. Содержание и общие требования к отчету 1. Отчет должен содержать и освещать следующие разделы: название работы; цель работы и исходные данные; необходимые схемы и рисунки; расчетные данные; таблицы с результатами эксперимента; выводы и заключение по работе. 2. Отчет (рис. 0.1) пишется от руки или набирается на компьютере. Цвет текста и формул – черный, синий или фиолетовый. 3. При выполнении чертежей (эскизов) или таблиц допускается применение форматов А2, А3. 4. Для обозначения абзацев пропускается пять знаков от линии левого поля листа. требования к тексту отчета 1. Разделы отчета нумеруются арабскими цифрами. Номер и название раздела разделяются точкой. Название раздела пишется прописными буквами посередине страницы. Переносы в названии разделов не допускаются. 2. Разделы могут включать в себя подразделы. Подразделы нумеруются арабскими цифрами в пределах раздела. Номер и название подраздела пишутся строчными буквами (кроме первой прописной) в следующем порядке: номер раздела, точка, номер подраздела, точка, название подраздела. Например:
3. Страницы отчета нумеруются, включая титульный лист, иллюстрации и приложения (рис. 0.1, а – г): номера страниц указываются в графе 7 (рис. 0.3 и рис. 0.4). 4. Отчет должен быть написан аккуратно, ясно и четко. Сокращения слов, кроме общепринятых, не допускаются. 5. Формулы, приводимые в отчете, сначала должны быть записаны в аналитическом виде с последующей расшифровкой всех символов, а потом с подставленными цифровыми значениями входящих в них величин и указанием результатов расчета, например, Е = 6. Когда по одной формуле выполняется несколько расчетов, то в отчете эта формула и расчеты по ней приводятся только один раз, а все остальные результаты расчетов сводятся в таблицу.
требования к иллюстрациям 1. Схемы и эскизы должны выполняться в соответствии с требованиями ЕСКД. 2. Рисунки и таблицы должны быть озаглавлены и пронумерованы. Под рисунком обязательна подпись. 3. Заголовки таблиц помещаются сверху, а названия рисунков – снизу. 4. Рисунки можно выполнять карандашом. 5. Для выполнения схем, рисунков и таблиц используется чертежный инструмент. 5. На каждый рисунок и таблицу необходимо дать ссылку в тексте и размещать иллюстрации или таблицы надо сразу после первого упоминания о них. 6. Таблицы следует располагать вертикально. Высота строк таблиц не менее 8 мм. Требования к оформлению отчета 1. Отчет по лабораторной работе (рис. 0.1, а – г) должен оформляться на белых листах бумаги формата А4 (210 2. Первым листом отчета является титульный лист (рис. 0.1, а), пример заполнения текста приведен на рис. 0.2. 3. Второй лист (рис. 0.1, б), текстовой части выполняется с основной надписью в соответствии с рис. 0.3. 4. Остальные листы (рис. 0.1, в – г) выполняются с основной надписью, согласно рис. 0.4. 5. В графе 2 (рис. 0.3, 0.4) указывается вид учебной работы – «лабораторная работа №…», в графе 1 – «название лабораторной работы», в графе 9 – название группы, в которой обучаются студенты. 5. Листы отчета должны быть скреплены (скрепкой, скобкой).
Рис. 0.1
Рис. 0.2
Рис. 03
ЛАБОРАТОРНАЯ РАБОТА № 1 СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ ЦЕЛЬ РАБОТЫ 1. Ознакомление с механизмами и приобретение практических навыков в составлении кинематических схем. 2. Определение степеней свободы механизма. 3. Классификация структурных групп механизма. Основные сведения Теория механизмов и машин (ТММ) разрабатывает и изучает научные проблемы построения и исследования механизмов и машин. Машина – это устройство, выполняющее механическое движение для преобразования энергии, материалов, информации с целью замены или облегчения физического и умственного труда человека. Механизм – это система взаимосвязанных тел (звеньев), предназначенная для преобразования заданных движений одного или нескольких тел в требуемое движение других тел. Задачей структурного синтеза является проектирование механизмов выбранной структуры по заданным кинематическим и динамическим условиям. Структурной схемой механизма называют безмасштабное графическое изображение механизма с применением условных обозначений звеньев и подвижных соединений. На структурных схемах подвижные соединения принято обозначать заглавными латинскими буквами, а звенья – арабскими цифрами. Кинематическая схема механизма (рис. 1.1, б) представляет собой изображение структурной схемы механизма, выполненное в масштабе µ l (м/мм).
а б Рис. 1.1. Механизм компрессора: а – конструктивная схема; б – кинематическая схема
Звенья плоских механизмов совершают движения в параллельных плоскостях. Стационарные механизмы образуют подвижные соединения с неподвижным в относительном движении звеном – стойкой. Деталь – это изделие, которое нельзя разделить на более мелкие части без нарушения возможности исполнения ее функций. Звеном называется деталь или несколько неподвижно соединенных между собой деталей, движущихся как одно целое. Звенья механизма на схемах изображаются упрощенно в виде линий или геометрических фигур. В зависимости от характера движения и назначения звенья имеют определенные названия. Перечислим звенья, используемые в рычажных механизмах. Кривошип – вращающееся звено механизма, которое совершает полный оборот вокруг оси, связанной со стойкой. Шатун – звено механизма, образующее кинематические пары только с подвижными звеньями. Ползун, толкатель – звено, образующее поступательную пару со стойкой. Камень – подвижное звено механизма, образующее поступательную пару с кулисой. Кулиса – подвижное звено механизма, являющееся направляющей для камня. Коромысло – звено механизма, которое совершает колебательные движения вокруг неподвижной оси, связанной со стойкой. Классификация звеньев рычажных механизмов приведена в табл. 1. Звенья механизма соединяются между собой кинематическими парами, обеспечивающими определенный характер их относительного движения. Кинематической парой называют идеальную удерживающую связь между двумя подвижными звеньями. Связь называется идеальной, если: · отсутствуют силы трения на поверхностях соприкосновения кинематических пар; · выполняются условия точности выполнения конструктивных размеров и правильности форм сопрягаемых элементов, образующих пару. Математически удерживающая связь выражена в виде равенства. Совокупность поверхностей, линий или точка звена, которые контактируют с другими звеньями, образуя кинематическую пару, называют элементом кинематической пары. Звено с наибольшим числом элементов кинематических пар называется базовым – Т. Поверхности и линии элементов, образующих кинематическую пару, могут быть сплошными или прерывистыми. В случае прерывистого контакта при одних и тех же кинематических характеристиках пары называют разнесенными. Обеспечить постоянство соединения (замыкания) звеньев кинематическими парами можно геометрическим или силовым способом. Кинематические пары с силовым замыканием называют открытыми, с геометрическим замыканием – закрытыми. Тип кинематической пары определяется характером соприкосновения элементов звеньев. Различают характер соприкосновения: высший – В, если звенья, образующие данную пару, касаются по точкам или линиям (высшей кинематической парой является сопряжение зубьев зубчатых колес 1 и 2, рис. 1.1), и низший – Н, по поверхности конечных размеров (цилиндрической, винтовой или плоской). По характеру относительного движения звеньев кинематические пары разделяются на поступательные (поршень и цилиндр), вращательные (вал и подшипник) и винтовые (пара «винт–гайка»). Класс пары определен числом степеней свободы звена кинематической пары в относительном движении (равен числу простейших движений одного звена относительно другого). Т а б л и ц а 1.1 Виды звеньев рычажных механизмов
Поступательная, вращательная и винтовая кинематические пары относятся к парам I класса, или одноподвижным, а зацепление двух сопряженных зубьев колес 1 и 2 представляет собой высшую пару II класса, или двухподвижную, (профили перекатываются и скользят один относительно другого). Классификация кинематических пар приведена в табл. 1.2.
Кинематические пары и их классификация
Связанная система звеньев, входящих в кинематические пары, называется кинематической цепью. В зависимости от того, в какое количество пар входит каждое звено, различают простые цепи (каждое звено входит не более чем в две пары) и сложные (имеется хотя бы одно звено, которое входит более чем в две пары), незамкнутые (есть звенья, которые входят только в одну пару) и замкнутые (каждое звено входит, по крайней мере, в две кинематические пары), плоские и пространственные. «Механизмом называется такая кинематическая цепь, в которой при заданном движении одного или нескольких звеньев относительно любого из них все остальные звенья совершают однозначно определенные движения» [1]. Шарнирным механизмом называют механизм, звенья которого соединены только вращательными парами. Число степеней свободы кинематической цепи механизма относительно звена, принятого за неподвижное, называется степенью подвижности и обозначается W. Для плоских механизмов подвижность определяется по формуле П.Л. Чебышева (1821–1894 гг.) W = 3 n – 2 p 1 – p 2 , где n – число подвижных звеньев; p 1 – число пар I класса; p 2 – число пар II класса; числовой коэффициент, равный 3, означает возможное количество неповторяющихся простейших движений, совершаемых звеном на плоскости, а коэффициенты 2 и 1 соответственно – число связей, налагаемых одно- и двухподвижными кинематическими парами на движения звеньев. Степень подвижности W определяет число независимых между собой обобщенных координат (законов движения), которыми нужно задаться, чтобы все подвижные звенья механизма относительно стойки совершали вполне определенные движения. Звено, которому приписывается одна или несколько обобщенных координат, называется начальным. У механизма (рис. 1.1) (n = 6, р 1 = 8, р 2 = 1) W = = При структурном анализе механизмов необходимо иметь в виду следующее. Кроме степеней свободы звеньев и связей (накладывают кинематические пары), активно воздействующих на характер движения механизмов, в них могут встречаться так называемые лишние степени свободы и пассивные связи, которые не влияют на характер движения механизма в целом [1–5]. Поэтому на этапе структурного исследования из кинематической цепи механизма удаляют звенья и кинематические пары, которым принадлежат лишние степени свободы и условия связи. При устранении избыточных связей снижают требования к точности изготовления кинематических пар, при этом контролируют значения дополнительных нагрузок от вредных колебаний (расчет конструкции на жесткость). Кинематическая цепь механизма (рис. 1.1) лишних степеней свободы и пассивных связей не имеет. Структурная классификация плоских механизмов с вращательными парами впервые была разработана русским ученым профессором Л.В. Ассуром (1878–1920 гг.), а затем развита академиком И.И. Артоболевским (1905–1977 гг.). Основной принцип образования механизмов сложной структуры состоит в следующем. Любой механизм может быть образован последовательным присоединением к механизму I класса кинематических цепей с нулевой степенью подвижности. Механизм I класса, или элементарный, нельзя более расчленить на части, способные самостоятельно преобразовывать движение. Степень подвижности любого механизма может быть представлена в форме W = W 1 + 0 + 0 +…, где W 1 – степень подвижности механизма I класса, состоящего из начального звена и стойки, объединенных кинематической парой. Простейшую кинематическую цепь с относительной W гр = 0, не распадающуюся на более простые кинематические цепи, удовлетворяющие тому же условию, называют структурной группой Ассура. При определении групп Ассура участие одних и тех же кинематических пар и звеньев в различных группах не допускается. Механизмы могут быть образованы также присоединением кинематических цепей с нулевой степенью подвижности к нескольким механизмам I класса. В этих случаях степень подвижности получаемых механизмов будет равна числу механизмов I класса, к которым производится такое присоединение, т. е. – числу начальных звеньев рассматриваемого механизма. Если в состав группы Ассура входят только пары I класса, то По классификации И.И. Артоболевского, номер класса группы равен числу кинематических пар, входящих в замкнутый контур, образованный внутренними кинематическими парами. Группы, состоящие из двух звеньев и трех кинематических пар, отнесены ко II классу. Порядок группы определяется числом элементов кинематических пар, которыми группа присоединена к механизму (или механизмам) I класса. Вид группы определен местом и количеством размещенных на ней вращательных и поступательных пар. Поступательные пары, как и вращательные, являются парами I класса, поэтому заменой вращательных пар поступательными могут быть получены различные виды групп Ассура. На рис. 1.2 приведено пять возможных видов группы II класса второго порядка, названных диадами Сильвестра.
Вид 1 Вид 2 Вид 3 Вид 4 Вид 5
Рис. 1.2. Виды группы Ассура II класса
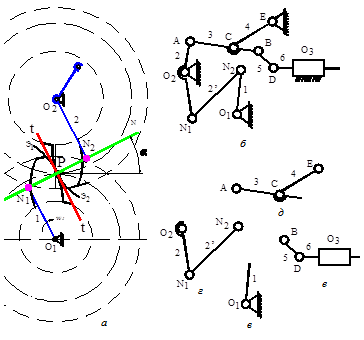
Класс механизма определяется наивысшим классом входящей в механизм группы Ассура. Плоские механизмы могут иметь в составе звенья, которые входят как в низшие I класса, так и в высшие кинематические пары II класса. Для структурной классификации таких механизмов необходимо пары II класса заменить парами I класса [1–5]. С точки зрения количества налагаемых связей, кинематики выходного звена и картины передачи усилий в плоских механизмах высшая пара II класса эквивалентна одному фиктивному звену, входящему в две низшие пары I класса. На рис. 1.3 структурная схема совмещена с кинематической, кроме того, на схеме зубчатых колес 1 и 2 показан процесс замены высшей кинематической пары, где для наглядности слева от схемы механизма изображена картина сопряжения зубьев, где Р – полюс зацепления, Э1 и Э2 – эвольвенты, NN – нормаль, tt – касательная к профилю зубьев проведенные через полюс зацепления.
Рис. 1.3. Структурная классификация компрессора: а – замена высшей кинематической пары (зубчатого зацепления); б – заменяющий механизм II класса; в – механизм I класса; г, д – группы Ассура
Механизм компрессора имеет в составе два зубчатых колеса 1 и 2, сопряженные зубья которых образуют пару II класса. До замены механизма, состоящего из пары зубчатых колес 1 и 2, он имеет W (1–2) = 3 n – 2 p 1 – p 2 = Эквивалентный заменяющий механизм (рис. 1.3, б) состоит из звеньев 1 и 2 (имитирующих колеса) и фиктивного эвена N 1 N 2 с двумя вращательными парами, длина которого Последовательность проведения структурного анализа механизма следующая: выделяем элементарный механизм I класса (рис. 1.3, а), который состоит из входного звена и стойки. Оставшуюся кинематическую цепь расчленяем на три группы Ассура II (рис. 1.3, г, д, е). Таким образом, механизм компрессора относится к механизмам II класса. Исследуемый механизм сложный, так как его структурная схема содержит звено с тремя кинематическими парами, называемыми вершинами t. В результате объединения между собой нескольких простых механизмов, которые могут существовать как на плоскости, так и в пространстве, получают сложные механизмы. Подвижность сложных механизмов W см определяют через сумму подвижностей простых механизмов, составляющих сложный, с учетом количества звеньев, участвующих в соединении простых.
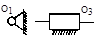
где j – порядковый номер общего звена; m – число звеньев соединяющих простые механизмы; i – число простых механизмов, образующих сложный; K – количество механизмов, объединенных j звеном. Подвижность простых механизмов компрессора (рис. 1.4. а, б, в) соответственно равна W 1 = 1, W 2 = 1, W 3 = 2. Количество механизмов, объединенных звеном 2, – K 2 = 2, звеном 3 – K 3 = 2 и звеном 4 – K 4 = 2.
Число элементов кинематических пар, посредством которых механизм присоединяются к стойке, обозначается S.
а б в Рис. 1.4. Простые механизмы компрессора
С учетом принятых обозначений одним из дополнительных требований, определяющих существование механизма, является условие, согласно которому количество кинематических пар механизма р равно половине сумм S и произведений количества вершин t звеньев на число звеньев nt с данным количеством вершин:
Тождественность частей дополнительного структурного требования компрессора, где Классификации звеньев, кинематических пар и структурных групп исследуемого механизма приведены в табл. 1.3–1.5.
|

 Ó Новосибирский государственный
Ó Новосибирский государственный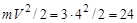 Н · м.
Н · м.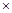 297 мм) с одной стороны.
297 мм) с одной стороны.



 Рис. 04
Рис. 04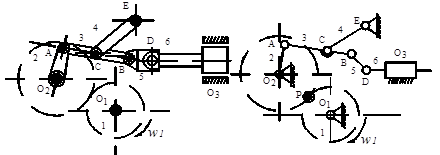
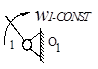

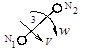


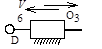
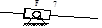
 Т а б л и ц а 1.2.
Т а б л и ц а 1.2.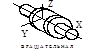
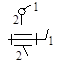
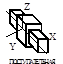

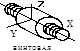

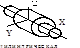

 5
5
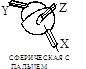

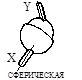
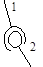
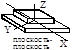
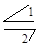



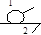
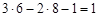 , следовательно, входное звено 1 является начальным, закон движения которого имеет вид φ1 = φ1(t), или ω1 = ω1(t), здесь φ1 – угол поворота, а ω1 – угловая скорость звена 1, t в конкретном случае – время.
, следовательно, входное звено 1 является начальным, закон движения которого имеет вид φ1 = φ1(t), или ω1 = ω1(t), здесь φ1 – угол поворота, а ω1 – угловая скорость звена 1, t в конкретном случае – время.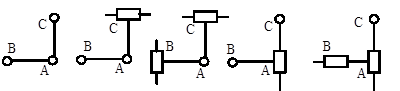
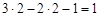 . Процесс замены высшей пары отражен на рис 1.3, а. Эвольвентные профили зубьев колес 1 и 2 соприкасаются в точке контакта Р – полюсе зацепления. Точки N 1 и N 2 являются центрами кривизны профилей, a ρ1 = N 1 Р и ρ2 = N 2 Р представляют собой радиусы кривизны эвольвент зубьев в точке Р, передача усилий с одного зуба на другой происходит по линии NN, которая является общей нормалью к профилям.
. Процесс замены высшей пары отражен на рис 1.3, а. Эвольвентные профили зубьев колес 1 и 2 соприкасаются в точке контакта Р – полюсе зацепления. Точки N 1 и N 2 являются центрами кривизны профилей, a ρ1 = N 1 Р и ρ2 = N 2 Р представляют собой радиусы кривизны эвольвент зубьев в точке Р, передача усилий с одного зуба на другой происходит по линии NN, которая является общей нормалью к профилям.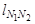 = ρ1 + ρ2, a W (1–2) заменяющего механизма равна 3 n – 2 p 1 =
= ρ1 + ρ2, a W (1–2) заменяющего механизма равна 3 n – 2 p 1 = 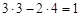 . В заменяющем механизме l 1 = O 1 N 1 = rb 1, а l 2 = O 2 N 2 = rb 2, где rb 1 и rb 2 – радиусы основных окружностей колес.
. В заменяющем механизме l 1 = O 1 N 1 = rb 1, а l 2 = O 2 N 2 = rb 2, где rb 1 и rb 2 – радиусы основных окружностей колес.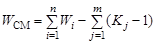 ,
,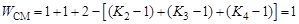 .
.
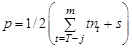 .
.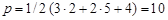 , подтверждает то, что исследуемая структура является механизмом.
, подтверждает то, что исследуемая структура является механизмом.


