Дисперсионные характеристики замедляющей структуры
Рассмотрим пути решения этой проблемы в следующей последовательности: сначала в общем виде рассмотрим дисперсионные свойства периодической передающей линии, проявляющиеся в наличии пространственных гармоник у основной волны передающей линии, затем выведем дисперсионное уравнение для основной волны, например, периодической структуры типа гребенки и, наконец, дадим диаграмму, отображающую дисперсию основной волны и ее гармоник, с помощью которой проиллюстрируем свойство отрицательной дисперсии у обратной волны, которая играет главную роль в ЛОВ. 1)При распространении электромагнитной волны в замедляющей системе, у которой пространственный период h и длина замедленной волны L соизмеримы, волна испытывает пространственно-периодическое возмущение, связанное с ее отражением от дискретных элементов системы. Последующая за этим интерференция отраженных волн с основным типом распространяющейся волны рождает сложное распределение электромагнитного поля вдоль замедляющей системы, которое может быть представлено в виде: E(x,y,z.t) = EMexp{i(wt - gz)}A(x,y,z), (2-62) гдеA(z) - периодическая функция с периодом, равным шагу замедляющей структуры h. Согласно теореме Флоке: A(x,y,z +nh) = A(x,y,z), (2-63) где n = 0; ±1; ±2... Периодическая функция (2-63) может быть представлена рядом Фурье по пространственным гармоникам: A(x,y,z) = Подставив (2-64) в (2-62), получим электрическое поле в виде ряда E(x,y,z.t) = Здесь: Em k = Emak- амплитуда гармоник. Выражение (g0 +2pm/h) = gm (2-66) будем рассматривать как постоянную распространения гармоник, а g0 - как постоянную распространения основной волны, когда m = 0. Из (2-66) получим выражение для фазовой скорости волны и ее гармоник: vфm = w/gm = w/[g0(w) +2pm/h]. (2-67) Номера гармоник m могут принимать как положительные, так и отрицательные значения, при этом с ростом m модуль фазовой скорости уменьшается, что облегчает условие синхронизации с пучком, поскольку позволяет снизить его скорость. При m<0 фазовая скорость гармоник отрицательна. C ростом m второй член в знаменателе (2-67) может превзойти g0(w) и тогда vфm будет стремиться к пропорциональности с w. Групповая скорость гармоник согласно определению и (2-66): vгрm = dw/dgm = dw/dg0 = vгр 0, (2-68) оказывается не зависящей от m и синхронна с групповой скоростью основной волны.
2)Дисперсионные свойства основной волны рассмотрим на примере замедляющей структуры типа гребенки (Рис.2-7а). Пусть высота зуба L, его толщина d и период повторения h по отношению к длине волны в вакууме l удовлетворяют неравенствам: l > L >> h >> d; l > L. (2-69) Выберем направление осей: x - по нормали к плоскости гребенки, y - вдоль пазов гребенки, z -в направлении распространения волны. Поле поверхностной волны при удалении от гребенки по x экспоненциально убывает, как это видно из уравнений для комплексных амплитуд: Ex1 = ig0pA exp(-px)exp(-ig0z), Hy1= iwe0pA exp(-px)exp(-ig0z), (2-70) Ez1 = p2A exp(-px)exp(-ig0z), Hx1 = Ey = Hz = 0. Поле в пазах гребенки, которые можно рассматривать как закороченные отрезки плоских волноводов длиной L имеет лишь две составляющие: Ez2 = Bsin[k(x + L)], Hy2 = iBZ0-1cos[k(x + L)], (2-71) где g0 = 2p/L - продольное волновое число замедленной волны; A, B - амплитудные коэффициенты, Z0 = (m0/e0)1/2 - волновое сопротивление вакуума. Приравнивая попарно тангенциальные электрические и магнитные составляющие поля на границе раздела, x = 0: Ex1 = Ex2; Hy1 = Hy2 и затем деля почленно одно уравнение на другое: Ex1/Hy1 = Ex2/Hy2 , (2-72) получаем характеристическое уравнение гребенки вида: p = k tg(kL). (2-73) Продольное волновое число замедленной волны g связано с поперечным волновым числом p и волновым числом плоской волны k характеристическим уравнением: g0 = (k2 + p2)1/2. (2-74) Исключив p из уравнений (2-73) и (2-74), получаем дисперсионное уравнение гребенки: g0 = k /cos (kL), (2-75) которое легко может быть преобразовано к виду: vф0 = c cos (kL). (2-76) Рис.2-7б иллюстрирует формулу (2-76) для r = µ, где r = L/h - параметр, отсутствующий в данном выводе, в виду того, что шаг гребенки согласно (2-69) принимался малым g0h <<1. Область существования замедленной волны находится в интервале 0 < kL < p/2 (т.е. 0 < L < l/4). В области p/2 < kL < p такой волны нет, так как правая часть (2-73) отрицательна. При L® 0, p® 0, vф ® с, по оси z распространяется обычная плоская волна. Строгая теория с учетом конечного значения периода решетки и его параметра r заметно корректирует дисперсию гребенки (Рис.2-7б). Учет высших пространственных гармоник показывает, что поверхностная волна может распространяться лишь при условии g0b £ p, когда b £ L/2. Попытка дальнейшего замедления приводит к срыву волны. Крайние правые точки на Рис.2-7б соответствуют именно этому условию g0b = p.
3) Проиллюстрируем сказанное диаграммой w - gm (Рис.2-8). Пусть пунктирная прямая отображает рабочую частоту w = w1, которая находится в середине полосы пропускания, ограниченной снизу частотой отсечки wс передающей линии (гребенчатой структуры, заключенной в волновод), а сверху - частотой wp, при которой сдвиг фаз на одну ячейку для основной гармоники (m=0) составляет p (L=lp/4), когда волна, входящая в периодическую структуру, полностью отражается назад, и ее распространение прекращается. Для основной волны зависимость w=f(g0) получим из (2-75). Наклон касательной к дисперсионной кривой в точке пересечения с прямой w = w1 соответствует vгр0(w1) (2-68), а наклон прямой, соединяющей начало координат с этой точкой, соответствует vф0(w1), что говорит о нормальной (положительной) дисперсии основной волны. На краях полосы пропускания касательные к дисперсионной кривой становятся горизонтальными, так как vгр0®0, распространение прекращается. Дисперсионные зависимости для гармоник основной волны m = ± 1, ±2...согласно (2-66) повторяются с периодом 2p/h вправо и влево по оси g. При этом касательные к точкам их пересечения с w=w1 имеют одинаковый наклон: vгрm(w1) = vгр0(w1), что вытекает из (2-68), а прямые из начала координат в эти же точки пересечения имеют разный наклон не только по величине, но и по знаку. С ростом m наклон уменьшается, что говорит об уменьшении фазовой скорости гармоник. Заполнение разрывов между дисперсионными кривыми симметричными пунктирными линиями не имеет физического смысла. Этот смысл появляется тогда, когда область отрицательных значений g мы переносим в область положительных значений для более компактного изображения графика или когда изменяем направление самой волны. Дисперсионная кривая гармоники m = -1 показывает, что ее групповая и фазовая скорости имеют противоположное направление, при этом она обладает аномальной дисперсией: dvф(-1)/dw>0, удовлетворяющей условию (2-61), которое не выполняется для основной волны, используемой в ЛБВ, в качестве генератора. Высшие гармоники с |m| >1 не имеют практического значения, так как их поле все сильнее прижимается к поверхности замедляющей структуры (x=0) и все слабее взаимодействует с электронным пучком, имеющим конечный поперечный размер по x.
|

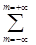 am(x,y) exp{- i2pmz/h}. (2-64)
am(x,y) exp{- i2pmz/h}. (2-64)


