Ошибки измерений
ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ЯДЕРНОЙ ФИЗИКЕ
Методические рекомендации к выполнению лабораторных работ
Издательство Томск 2007 ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
Ошибки измерений
На результаты экспериментов помимо статистических флуктуации, связанных с вероятностной природой явления, оказывают влияние случайные воздействия, возникающие в процессе эксперимента и обработки. Совокупность внешних возмущений увеличивает разброс результатов и вызывает смещение среднего значения. Последнее усугубляется действием целого ряда систематических причин («сдвинутая» шкала приборов, плохая геометрия опыта и т. д.). Каждая из случайных причин обычно подчиняется собственному распределению. Таким образом, результаты измерений будут описываться распределением, возникающим как наложение многих частных распределений. В итоге, однако, форма его будет приближаться к гауссовой, если только нет каких-либо превалирующих причин. Это обстоятельство является следствием так называемой центральной предельной теоремы теории вероятности, утверждающей, что действие большого числа причин с интенсивностями воздействия примерно одного порядка приводит к нормальному распределению величин, возникающих под влиянием этих воздействий. В опыте отклонение результатов от среднего значения интерпретируется как ошибка измерений. При этом различают случайные и систематические ошибки, обусловленные соответственно случайными и систематическими причинами. Однако понятием «ошибка измерений» следует пользоваться с известной осторожностью. Если разброс значений, возникающий в процессе самого эксперимента, и может трактоваться как ошибка измерений, то неопределенность результатов, связанная с природой исследуемого процесса, позволяет лишь судить о статистических закономерностях рассматриваемого явления и не может называться собственной ошибкой. Таким образом, следуя одностороннему определению ошибки, ее можно «обнаружить» даже в условиях идеального эксперимента, в то время как расхождение экспериментальных данных будет отражать объективную реальность явления. Хотя, конечно, можно упомянуть класс экспериментов по измерению абсолютных констант (заряд, масса, спин элементарных частиц и т. д.), в которых разброс значений при определении этих величин, по-видимому, нужно отнести к «чистым» ошибкам измерения. К сожалению, на практике погрешности методики измерения не всегда поддаются оценке. Поэтому в настоящее время вместо ошибки принято указывать доверительный интервал, в пределах которого с определенной вероятностью (доверительной вероятностью) можно ожидать значения исследуемых величин в условиях предлагаемой методики измерения. Для случайной величины х доверительный интервал
Вероятность (1− α;) называют также коэффициентом надежности, а величину α − уровнем значимости. Надежным критерием для оценки доверительного интервала при заданном уровне значимости является среднеквадратичное отклонение σ;, квадрат которого есть дисперсия, характеризующая рассеивание значений случайной величины в окрестности ее среднего значения (если, конечно, существует Допустим, что при измерениях получены результаты ξ;1, ξ;2,…, ξn. Тогда в качестве оценки среднего значения
Усредненный результат серии измерения меньше отклоняется от точного значения, чем отдельные измерения; дисперсия среднего значения в n раз меньше дисперсии отдельных измерений, т. е.
Соотношения (1.2) тем точнее, чем больше n.
|

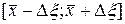 соответствует доверительной вероятности (1− α;), если
соответствует доверительной вероятности (1− α;), если . (1.1)
. (1.1) и σ;2).
и σ;2). ,
, 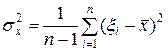 . (1.2)
. (1.2) .
.


