ПРИЛОЖЕНИЕ Б. Частица в прямоугольной потенциальной яме
Для простоты будем рассматривать прямоугольную потенциальную яму бесконечно большой глубины и конечной ширины a (рис. Б). Потенциальная энергия частицы (с массой μ;) при x < 0 и x > a должна быть бесконечно велика, поэтому ее волновая функция за пределами ямы обращается в нуль. Внутри ямы, где U (x) = 0, уравнение Шредингера
Введем следующее обозначение:
Тогда уравнение Шредингера будет выглядеть как
Его решением является функция
Это решение должно обращаться в нуль на границах потенциальной ямы. В результате В = 0 и
Отсюда получим
где n = 1, 2, 3 и т.д. Решение n = 0 следует отбросить как лишенное физического смысла. В этом случае волновая функция равна нулю тождественно, т.е. при всех значениях x. Но поскольку квадрат модуля волновой функции – это плотность вероятности обнаружить частицу в точке x, вероятность найти частицу где-либо в пространстве при n = 0 равна нулю (такой частицы просто нет). Число n называется квантовым числом и равно целому числу длин полуволн де Бройля частицы
со средеквадратичным значением импульса
Остановимся подробнее на свойствах ψ; -функций. Четность состояний, определяемая в данном случае как свойство ψ; -функции менять или сохранять знак при замене координаты x на a – x, чередуется: функция ψ;1 нижнего по энергии (основного) состояния является четной, функция ψ;2 следующего (первого возбужденного) состояния – нечетной, и т.д. Волновые функции частицы четны или нечетны лишь в одномерной потенциальной яме, симметричной относительно середины. Функция ψ;1 не имеет узлов (т.е. не обращается в нуль) на всем интервале 0 < x < a. Функция ψ;2 имеет один узел, ψ;3 – два узла, и.т.д. Число связанных состояний в потенциальной яме конечной глубины определяется ее глубиной (для бесконечной ямы оно бесконечно). В области, где En < U (x), волновые функции, хотя и быстро стремятся к нулю, но не обращаются в нуль тождественно (см. ПРИЛОЖЕНИЕ В): это происходит только при U → +∞. Все это – общие, не зависящие от конкретного вида потенциала, свойства одномерного финитного движения – движения, совершающегося (по классическим представлениям) в ограниченной области пространства.
|

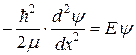 .
.
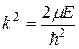 .
.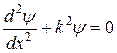 .
.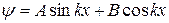 .
.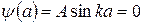 .
.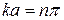 , т.е.
, т.е.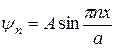
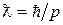
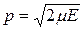 на отрезке длиной a (рис. Б). Энергия, соответствующая волновой функции с квантовым числом n, равна
на отрезке длиной a (рис. Б). Энергия, соответствующая волновой функции с квантовым числом n, равна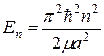 .
.


