ПРИЛОЖЕНИЕ В. Квантовый гармонический осциллятор
Линейным, или одномерным гармоническим осциллятором называется частица, движущаяся в потенциале
(величину k называют силовой постоянной). Согласно классической механике, такая частица совершает в направлении х гармонические колебания с циклической частотой
Если ввести безразмерные величины энергии и координаты
то оно преобразуется в
При ν; = 1 решением этого уравнения является функция
в чем легко убедиться путем проверки. Это решение соответствует основному состоянию осциллятора, так как оно не имеет узлов. Энергия в основном состоянии равна Решение, соответствующее n -му возбужденному состоянию должно иметь n (1, 2, 3 и т.д.) узлов. Такое число узлов имеет функция
где Используя то, что
после подстановки (В.2) в уравнение (В.1) получим
что дает возможные значения энергии
Таким образом, уровни энергии квантового линейного гармонического осциллятора эквидистантны, т.е. находятся на равных расстояниях друг от друга (рис. В).
|
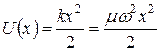
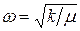. Уравнение Шредингера для одномерного осциллятора
.
,
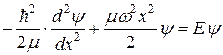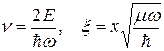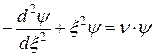. (В.1)
,
.
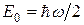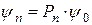, (В.2)
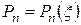– полином n -й степени с некратными вещественными корнями.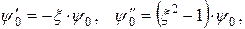
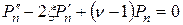. (В.3)
Второе и третье слагаемые здесь являются полиномами степени n. Тогда, чтобы определить ν;, достаточно сравнить коэффициенты при старших членах этих полиномов. Если коэффициент при ξ n в третьем слагаемом равен a (ν;–1), то во втором слагаемом он будет равен –2 an. Так как соотношение (В.3) должно выполняться тождественно, при всех значениях ξ;, то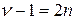
,
.
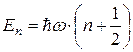