Последовательность независимых испытаний. Формула Бернулли.
Если производитсяс несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Наступление события А обычно называют успехом, а ненаступление - неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p), p – успех. Вероятность того, что в n независимых испытаниях успех наступит ровно k раз, выражается формулой Бернулли: Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит k раз и не наступит n-kраз, по теореме умножения вероятностей независимых событий, равна pkqn-k. Таких сложных испытаний может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. Ckn. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в испытаниях n) равна вероятности одного сложного события, умноженной на их число:
|
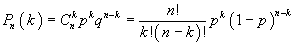про стрелять три вероятность попасть 2 раза
