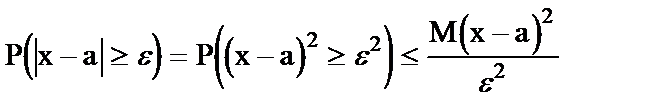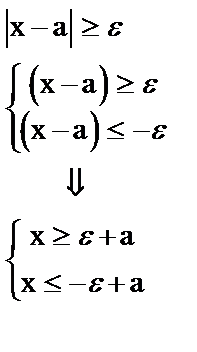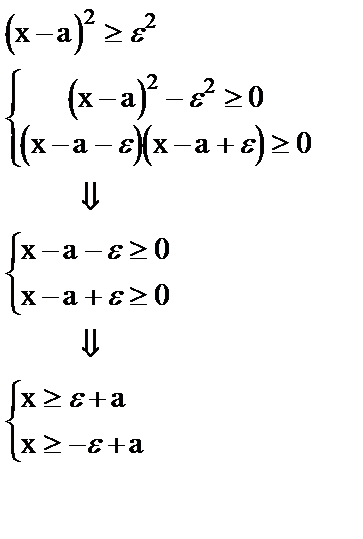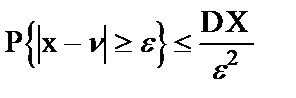Неравенство Чебышева
Рассмотрим случайную величину X с конечным мат. ожиданием и дисперсией Для любого неотрицательного числа t вероятность наступления события
Пусть Z - непрерывная случайная величина с плотностью вероятности f(Z). Пространство событий величины Z (0; ¥). Тогда имеет место неравенство
Доказать неравенства
Рассмотрим два сложных события
a - произвольное действительное число. Показать самим, что x - удовлетворяет и одному и другому неравенству. Тогда
В данном случае Равномерность неравенств при e>0
или, в частности, при a=n=MX
при e=st справедливо неравенство Чебышева. Метод Монте-Карло используется очень часто, порой некритично и неэффективным образом. Он имеет некоторые очевидные преимущества: а) Он не требует никаких предложений о регулярности, за исключением квадратичной интегрируемости. Это может быть полезным, так как часто очень сложная функция, чьи свойства регулярности трудно установить. б) Он приводит к выполнимой процедуре даже в многомерном случае, когда численное интегрирование неприменимо, например, при числе измерений, большим 10. в) Его легко применять при малых ограничениях или без предварительного анализа задачи. Он обладает, однако, некоторыми недостатками, а именно: а) Границы ошибки не определены точно, но включают некую случайность. Это, однако, более психологическая, чем реальная, трудность. б) Статическая погрешность убывает медленно. в) Необходимость иметь случайные числа. Список литературы Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов втузов. – 3-е изд., перераб. И доп. – М.: Высш. школа, 1979г. Ермаков С. М. Методы Монте-Карло и смежные вопросы. М.: Наука, 1971г. Севастьянов Б. А. Курс теории вероятностей и математической статистики. – М.:Наука,1982г. Математика. Большой энциклопедический словарь / Гл. ред. Ю. В. Прохоров. – М.: Большая Российская энциклопедия,1999г. Гмурман В. Е. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. Изд. 5-е, перераб. и доп. М., «Высш. школа», 1977. Гмурман В.Е. Теория вероятностей и математическая статистика, — М.: Высшее образование. 2005 Gnedin, Sasha "The Mondee Gills Game." журнал The Mathematical Intelligencer, 2011 http://www.springerlink.com/content/8402812734520774/fulltext.pdf vos Savant, Marilyn. Колонка «Ask Marilyn», журнал Parade Magazine от 17 февраля 1990. vos Savant, Marilyn. Колонка «Ask Marilyn», журнал Parade Magazine от 26 февраля 2006. Bapeswara Rao, V. V. and Rao, M. Bhaskara. «A three-door game show and some of its variants». Журнал The Mathematical Scientist, 1992, № 2. Tijms, Henk. Understanding Probability, Chance Rules in Everyday Life. Cambridge University Press, New York, 2004. (ISBN 0-521-54036-4) ↑ Колмогоров А. Н. Глава IV. Математические ожидания; §3. Неравенство Чебышева // Основные понятия теории вероятностей. — 2-е изд. — М.: Наука, 1974. — С. 63—65. — 120 с. ↑ Боровков А. А. Глава 4. Числовые характеристики случайных величин; §5. Дисперсия // Теория ве Гурский Д., Турбина Е. Mathcad для студентов и школьников. Популярный самоучитель. — СПб.: Питер, 2005. — С. 340. — ISBN 5469005259 Орлов А. И. Дисперсия случайной величины // Математика случая: Вероятность и статистика — основные факты. — М.: МЗ-Пресс, 2004. роятностей. — 5-е изд. — М.: Либроком, 2009. — С. 93-94. — 656 с. http://www.parny.by.ru/ http://www.zadachi.org.ru
|

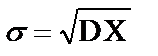

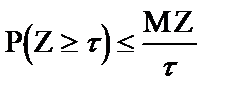
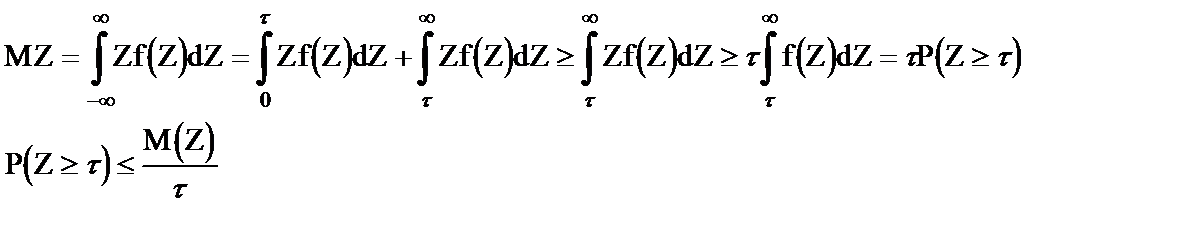
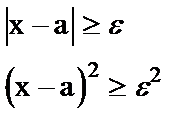
 справедливо
справедливо