Вычисление кратных интегралов методом Монте-Карло.
Пусть функция
Геометрически число I представляет собой (m+1)-мерный объём прямого цилиндроида в пространстве Преобразуем интеграл (1) так, чтобы новая область интегрирования целиком содержалась внутри единичного m-мерного куба. Пусть область S расположена в m-мерном параллелепипеде
Сделаем замену переменных Тогда, очевидно, m-мерный параллелепипед (2) преобразуется в m-мерный единичный куб и, следовательно, новая область интегрирования σ, которая находится по обычным правилам, будет целиком расположена внутри этого куба. Вычисляя якобиан преобразования, будем иметь:
где Укажем способ вычисления интеграла (5/) методом случайных испытаний. Выбираем m равномерно распределённых на отрезке [0, 1] последовательностей случайных чисел:
Точки 1. 2. (для удобства мы здесь изменяем нумерацию точек). Заметим, что относительно границы Г области σ следует заранее договориться, причисляются ли граничные точки или часть их к области σ, или не причисляются к ней. В общем случае при гладкой границе Г это не имеет существенного значения; в отдельных случаях нужно решать вопрос с учётом конкретной обстановки. Взяв достаточно большое число n точек Теорема Колмогорова
Любая числовая скалярная функция, которая удовлетворяет свойствам, которым удовлетворяет функция распределения, является функцией распределения и однозначно задает вероятностное пространство вида:
- борелевская алгебра; P - мера на борелевской алгебре; R1 - числовая скалярная ось. Введем функцию F(x)
Эта функция определена для всех x, неубывающая, непрерывная сверху. Показать самим, что такая функция однозначно задает счетно-аддитивную меру на поле, порожденном всеми полуинтервалами ненулевой длины. Докажем, что 0<F(x)<1 Согласно терминологии, если функция y=f(x) непрерывна на отрезке [a, b], то она ограничена. Поскольку наша функция не убывающая, то максимум и минимум она соответственно будет иметь такой:
т.е. 0<F(x)<1.
2. Пусть имеем следующие функции. Построим борелеву алгебру на поле, тогда по теореме о продолжении счетно-аддитивная функция, определенная на поле, без изменения аксиом теории вероятности, однозначно распространяется на все элементы борелевой алгебры, не принадлежащие полю. Т.о. вероятностное пространство построено, теорема доказана. Смысл теоремы. Теорема Колмогорова позволяет утверждать, что если вы исследуете случайную величину, то не надо строить абстрактное пространство элементарных событий, -алгебру, счетно-аддитивную меру, конкретный вид функции X1, X2,..., Xn
|

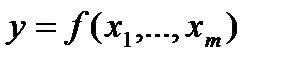 непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл
непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл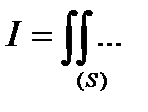
 . (1)
. (1) , построенного на основании S и ограниченного сверху данной поверхностью
, построенного на основании S и ограниченного сверху данной поверхностью  , где
, где  .
.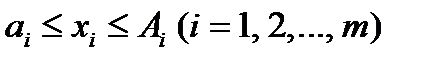 . (2)
. (2)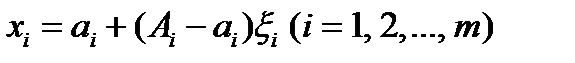 . (3)
. (3)
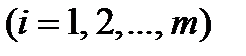 (4)
(4) . Таким образом,
. Таким образом, 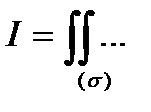
 , (5)
, (5)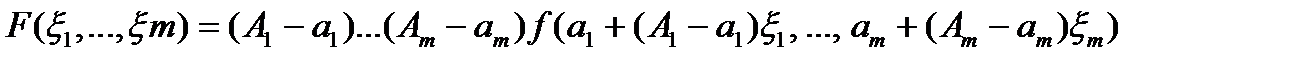 . Введя обозначения
. Введя обозначения 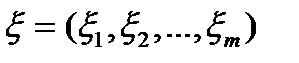 и
и 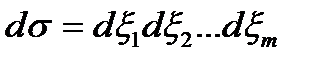 , запишем интеграл (5) короче в следующем виде:
, запишем интеграл (5) короче в следующем виде: 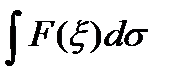 . (5/)
. (5/)
 можно рассматривать как случайные. Выбрав достаточно большое N число точек
можно рассматривать как случайные. Выбрав достаточно большое N число точек  , проверяем, какие из них принадлежат области σ (первая категория) и какие не принадлежат ей (вторая категория). Пусть
, проверяем, какие из них принадлежат области σ (первая категория) и какие не принадлежат ей (вторая категория). Пусть при i=1, 2, …, n (6)
при i=1, 2, …, n (6)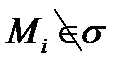 при i=n+1, n+2, …,N (6/)
при i=n+1, n+2, …,N (6/) , приближённо можно положить:
, приближённо можно положить:  ; отсюда искомый интеграл выражается формулой
; отсюда искомый интеграл выражается формулой  , где под σ понимается m-мерный объём области интегрирования σ. Если вычисление объёма σ затруднительно, то можно принять:
, где под σ понимается m-мерный объём области интегрирования σ. Если вычисление объёма σ затруднительно, то можно принять: 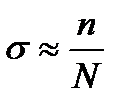 , отсюда
, отсюда  . В частном случае, когда σ есть единичный куб, проверка становится излишней, то есть n=N и мы имеем просто
. В частном случае, когда σ есть единичный куб, проверка становится излишней, то есть n=N и мы имеем просто 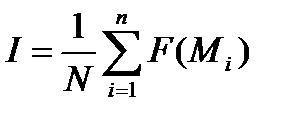 .
.
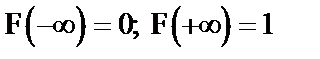

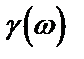 . Нашей задачей будет лишь то, что считая R1 - числовой скалярной осью - пространство элементарных событий, мы должны найти функцию распределения F(x), использую статистику: результата конкретного испытания над случайной величиной:
. Нашей задачей будет лишь то, что считая R1 - числовой скалярной осью - пространство элементарных событий, мы должны найти функцию распределения F(x), использую статистику: результата конкретного испытания над случайной величиной:


