Метод Монте-Карло и его применение
Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений. Возникновение идеи использования случайных явлений в области приближённых вычислений принято относить к 1878 году, когда появилась работа Холла об определении числа с помощью случайных бросаний иглы на разграфлённую параллельными линиями бумагу. Существо дела заключается в том, чтобы экспериментально воспроизвести событие, вероятность которого выражается через число , и приближённо оценить эту вероятность. Отечественные работы по методу Монте-Карло появились в 1955-1956 годах. С того времени накопилась обширная библиография по методу Монте-Карло. Даже беглый просмотр названий работ позволяет сделать вывод о применимости метода Монте-Карло для решения прикладных задач из большого числа областей науки и техники. Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались мало пригодными. Далее его влияние распространилось на широкий класс задач статистической физики, очень разных по своему содержанию. Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики (например, развитие методов численного интегрирования) и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Это объясняется как естественностью получения ответа с некоторой заданной вероятностью в задачах с вероятностным содержанием, так и существенным упрощением процедуры решения. Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину Х, математическое ожидание которой равно а: М(Х)=а. Практически же поступают так: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое
Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину Х, как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*.
Математическое ожидание, дисперсия. Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятность., где Х – случайная величина, Математическое ожидание приближённо равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины. Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания: Средним квадратичным отклонением случайной величины Х называют квадратный корень из дисперсии:
|

 и принимают x в качестве оценки (приближённого значения) a* искомого числа a:
и принимают x в качестве оценки (приближённого значения) a* искомого числа a: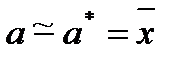 .
.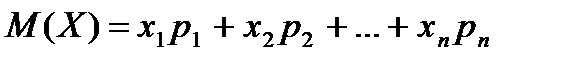
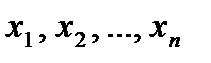 - значения, вероятности которых соответственно равны
- значения, вероятности которых соответственно равны 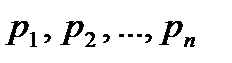 .
. .
.



