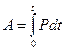Величина
- работа силы Таким образом, работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии этой частицы:
Формула (4.3) для кинетической энергии частицы справедлива как в инерциальной, так и в неинерциальной системе отсчет а. При переходе из одной системы отсчета в другую, движущуюся относительно первой с некоторой скоростью  , скорость частицы меняется, следовательно, меняется и кинетическая энергия. , скорость частицы меняется, следовательно, меняется и кинетическая энергия.
Рассмотрим две системы отсчета: · · систему отсчета Из рисунка 4.1 видно, что радиус-векторы где Возведем это равенство в квадрат: Подставим значение
Здесь
Очевидно, Поэтому, если в качестве
Это теорема Кёнига: кинетическая энергия механической системы равна сумме кинетической энергии той же системы в ее движении относительно центра масс и кинетической энергии, которую имела бы рассматриваемая система, двигаясь поступательно со скоростью центра масс. Из теоремы Кёнига следует, что кинетическая энергия твердого тела равна сумме его кинетической энергии в поступательном движении со скоростью центра масс тела и кинетической энергии вращения этого тела вокруг центра масс Выражение (4.4) можно представить в виде: где · если · если · При
На рис.4.2 представлен график проекции силы на направление перемещения И з рисунка видно, что · элементарная работа · работа Отметим следующее важное обстоятельство: формула (4.4) справедлива не только для частицы, но и вообще для любого тела (или системы тел). Надо только иметь в виду, что под dr (или ds) следует понимать перемещение точки приложения силы F. Игнорирование этого обстоятельства зачастую приводит к ошибочным результатам.
· над осью s берется со знаком плюс (она соответствует положительной работе), · а площадь фигуры под осью s —со знаком минус (она соответствует отрицательной работе).
Пусть на тело действует одновременно несколько сил Из дистрибутивности скалярного произведения векторов вытекает, что работа
- работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Очевидно, элементарное перемещение поэтому выражение для э лементарной работы (4.4) принимает вид: Тогда работа, совершаемая за промежуток времени от
Единицей работы в СИ является джоуль (Дж). Джоуль — это работа силы в 1 Н на пути 1 м (при условии, что направление силы совпадает по направлению с перемещением), или 1 Дж =1 Н м. Для характеристики скорости, с которой совершается работа, вводят величину, называемую мощностью. Мощность, по определению, — это работа, совершаемая силой за единицу времени. Если за промежуток времени dt сила
Учитывая, что Таким образом, мощность, развиваемая силой F, равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения данной силы. Как и работа, мощность — величина алгебраическая. Зная мощность силы F, можно найти и работу, которую совершает эта сила за промежуток времени t. В самом деле, представив подынтегральное выражение в формуле (4.2) в виде
Единицей мощности в СИ является ватт (Вт), равный джоулю в секунду (Дж/с). Когда говорят о работе (или мощности), то необходимо в каждом конкретном случае четко указывать или представлять себе, работа какой именно силы (или сил) имеется в виду. В противном случае, как правило, неизбежны недоразумения. Работа и мощность силы зависят от выбора системы отсчета.
|

 (4.4)
(4.4) на пути
на пути 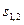 .
. . (4.5)
. (4.5)
 инерциальную
инерциальную 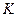
 , движущуюся относительно
, движущуюся относительно 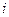 -той материальной точки в системах отсчета
-той материальной точки в системах отсчета  ,
,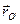 - радиус-вектор в системе
- радиус-вектор в системе  (начала отсчета координат в системе
(начала отсчета координат в системе  .
.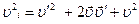 .
.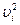 в формулу кинетической энергии механической системы, получаем кинетическую энергию относительно системы
в формулу кинетической энергии механической системы, получаем кинетическую энергию относительно системы  ,или
,или 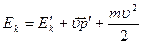 .
. - масса всей системы,
- масса всей системы, - импульс механической системы в
- импульс механической системы в  - кинетическая энергия системы в
- кинетическая энергия системы в  , где
, где  - скорость центра масс системы в
- скорость центра масс системы в  и
и 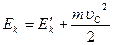 .
.
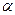 - угол между направлениями силы и перемещения.
- угол между направлениями силы и перемещения.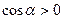 ), работа положительна;
), работа положительна; ), работа отрицательна;
), работа отрицательна;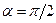 работа равна нулю.
работа равна нулю. Выражению (4.4) можно придать наглядный геометрический смысл.
Выражению (4.4) можно придать наглядный геометрический смысл.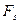 как функции положения частицы на траектории.
как функции положения частицы на траектории. численно равна площади заштрихованной полоски,
численно равна площади заштрихованной полоски, на пути 1-2 численно равна площади фигуры, ограниченной кривой
на пути 1-2 численно равна площади фигуры, ограниченной кривой  Из рисунка видно, что элементарная работа численно равна площади заштрихованной полоски, а работа А на пути от точки 1 до точки 2 — площади фигуры, ограниченной кривой, ординатами 1 и 2 и осью s. При этом площадь фигуры
Из рисунка видно, что элементарная работа численно равна площади заштрихованной полоски, а работа А на пути от точки 1 до точки 2 — площади фигуры, ограниченной кривой, ординатами 1 и 2 и осью s. При этом площадь фигуры .
. , совершаемая результирующей силой на пути
, совершаемая результирующей силой на пути 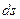 , может быть представлена в виде:
, может быть представлена в виде:
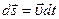 ,
,
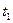 до
до  , будет равна
, будет равна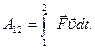
 , то мощность, развиваемая этой силой в данный момент времени, есть
, то мощность, развиваемая этой силой в данный момент времени, есть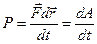
 , получаем
, получаем 
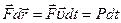 , получим
, получим