Потенциальное поле сил. Консервативные силы.
Если частица в каждой точке пространства подвержена воздействию других тел, то говорят, что эта частица находится в поле сил. Например, · вблизи поверхности Земли частица находится в поле силы тяжести. · Если в каждой точке поля сила, действующая на частицу, одинакова по величине и направлению, поле называется однородным. Силовое поле, которое можно описать с помощью функции
называется потенциальным. Функция Если поле не изменяется со временем, оно называется стационарным, в этом случае Добавление к функции Вектор с компонентами ( Из определения градиента следует, что поэтому в случае потенциального силового поля имеем:
Работа силы, удовлетворяющей условию (4.7), равна
т.е. представляет собой полный дифференциал функции Проинтегрировав выражение (4.8) по некоторой траектории от точки 1 до точки 2, получаем:
Форма траектории, по которой осуществлялось интегрирование, была совершенно произвольной. Таким образом, работа, совершаемая над частицей силами стационарного потенциального поля, · не зависит от пути, по которому двигалась частица, · определяется только начальным и конечным положениями частицы в пространстве. · работа таких сил на замкнутом пути равна нулю. Силы, работа которых не зависит от пути, по которому частица переходит из одного положения в другое, называются консервативными. Следовательно, силы, действующие на частицу в стационарном потенциальном поле, являются консервативными.
Из независимости работы консервативных сил от пути вытекает, что работа таких сил на замкнутом пути равна нулю.
разобьем произвольный замкнутый путь (рис.4.4) на две части: - путь 1, по которому частица переходит из точки 1 в точку 2, - и путь Работа на всем замкнутом пути равна сумме работ, совершаемых на каждом из участков:
Очевидно, работы Поэтому равенство (4.10) можно записать в виде: Так как работа не зависит от пути, то
Кроме консервативных сил существуют неконсервативные силы. К ним относятся диссипативные силы, переводящие механическую энергию во внутреннюю. Это силы · трения, сопротивления среды, · гироскопические силы, перпендикулярные скорости (сила Кориолиса, сила Лоренца), работа которых всегда равна нулю. Для неконсервативных сил соотношение (4.7) не выполняется.
Эта сила в любой точке имеет одинаковые величину и направление – вниз по вертикали (рис.4.5). Поэтому, независимо от того, по какому из путей 1 или II движется частица, работа определяется выражением:
Из рис.4.5 видно, что проекция вектора Тогда работа Это выражение не зависит от пути, следовательно, сила тяжести консервативна. Силы, действующие на частицу в центральном поле, также консервативны (рис.4.6).
Проекция Работа на всем пути Это выражение · зависит только от вида функции · не зависит от вида траектории. Следовательно, центральная сила консервативна.
|

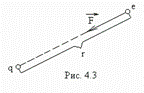 В электрическом поле неподвижного точечного заряда
В электрическом поле неподвижного точечного заряда  на заряженную частицу действует поле, характерное тем, что направление силы, действующей на частицу в любой точке пространства, проходит через неподвижный центр (заряд
на заряженную частицу действует поле, характерное тем, что направление силы, действующей на частицу в любой точке пространства, проходит через неподвижный центр (заряд  . Такое поле называется центральным (рис.4.3).
. Такое поле называется центральным (рис.4.3). такой, что
такой, что (4.6)
(4.6)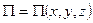 .
. , вычисляемых по формулам (4.6). Поэтому потенциальная функция определяется с точностью до произвольной аддитивной постоянной. Однако при фиксированном значении этой постоянной
, вычисляемых по формулам (4.6). Поэтому потенциальная функция определяется с точностью до произвольной аддитивной постоянной. Однако при фиксированном значении этой постоянной 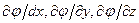 , где
, где 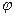 - скалярная функция координат, называется градиентом функции
- скалярная функция координат, называется градиентом функции 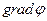 либо
либо 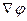
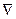 называется оператором набла,
называется оператором набла,  ,
, . (4.7)
. (4.7)
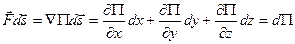 , (4.8)
, (4.8)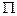 .
.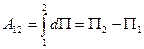 . (4.9)
. (4.9)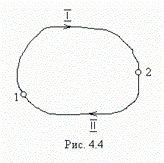 Чтобы доказать это,
Чтобы доказать это,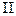 , по которому частица переходит из точки 2 в точку 1. При этом точки 1 и 2 выбраны произвольно.
, по которому частица переходит из точки 2 в точку 1. При этом точки 1 и 2 выбраны произвольно.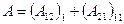 . (4.10)
. (4.10)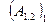 и
и  отличаются только знаком. Действительно, изменение направления движения на обратное приводит к замене
отличаются только знаком. Действительно, изменение направления движения на обратное приводит к замене  на -
на -  изменяет знак на обратный.
изменяет знак на обратный.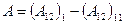 .
.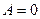 .
.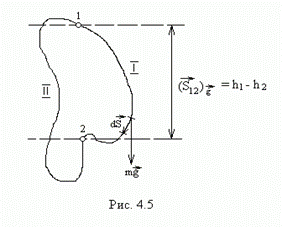 Докажем, что сила тяжести является консервативной.
Докажем, что сила тяжести является консервативной.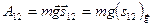
 на направление
на направление  равна разности высот
равна разности высот 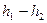 .
.
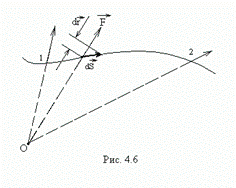 Элементарная работа центральной силы на пути
Элементарная работа центральной силы на пути 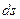 равна
равна  .
.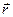 , она равна приращению расстояния частицы до центра силового поля О:
, она равна приращению расстояния частицы до центра силового поля О: 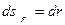 .
.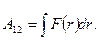
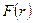 и от значений
и от значений  и
и 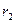 .
. 


