Кинетическая энергия. Работа. Мощность.
Энергия – скалярная величина · является количественной мерой различных форм движения материи и соответствующих им взаимодействий. Движение – неотъемлемое свойство материи. Поэтому любое тело, любая система тел и полей обладают энергией. · характеризует возможные изменения движения системы. Эти изменения происходят вследствие взаимодействия между частями системы, а также между системой и внешней средой. Для различных форм движения и соответствующих им взаимодействий в физике вводят различные виды энергии – механическую, внутреннюю, электрическую и т.д. В механике различают два вида механической энергии: кинетическую и потенциальную. Кинетической энергией механической системы называется энергия механического движения этой системы. Изменение механического движения системы происходит только под действием приложенной к ней силы. Поэтому дляотыскания вида функции кинетической энергии воспользуемся вторым законом Ньютона. Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки). Уравнение движения частицы умножим на перемещение получаем Здесь Левую часть выражения (4.1) приведем к виду:
Тогда имеем: Если система замкнута, то
Эта величина и называется кинетической энергией. В случае изолированной частицы кинетическая энергия сохраняется и является интегралом движения. Умножив на массу частицы Кинетическая энергия механической системы, состоящей из Если на частицу действует сила Согласно (4.2), приращение кинетической энергии частицы за время Величина Проинтегрировав выражение (4.2) вдоль траектории от точки 1 до точки 2, получаем:
|

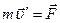
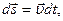
 . (4.1)
. (4.1)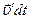 - приращение скорости частицы
- приращение скорости частицы  за время
за время 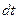 .
. (4.2)
(4.2)
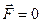 , и
, и  , а сама величина остается постоянной.
, а сама величина остается постоянной.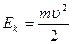 (4.3)
(4.3)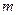 числитель и знаменатель выражения (4.3) и воспользовавшись определением импульса, получаем:
числитель и знаменатель выражения (4.3) и воспользовавшись определением импульса, получаем: 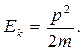
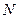 частиц, равна сумме кинетических энергий отдельных частиц:
частиц, равна сумме кинетических энергий отдельных частиц: 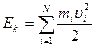 .
. , кинетическая энергия не остается постоянной.
, кинетическая энергия не остается постоянной.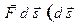 - перемещение частицы за время
- перемещение частицы за время 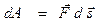 называется работой, совершаемой силой
называется работой, совершаемой силой 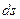 , где
, где  .
. .
.


