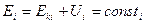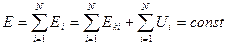Потенциальная энергия во внешнем поле сил.
Из выражения (4.9) следует, что работа равна приращению потенциальной функции, и эта работа идет на приращение кинетической энергии частицы, как показывает (4.5). Таким образом,
Перейдем от функции
Тогда из (4.11) получаем: Полученный результат означает, что величина Функция Таким образом, потенциальная энергия · х арактеризует взаимодействие частицы с полем сил · зависит от положения частицы в этом поле, т.е. от координат. Величину Из выражения (4.9) с учетом (4.12) получаем:
- работа, совершаемая над частицей силами консервативного поля, равна убыли потенциальной энергии частицы, т.е. работа совершается за счет запаса потенциальной энергии. Выражение (4.7) с учетом (4.12) принимает вид:
– сила, действующая на частицу в стационарном поле сил, равна градиенту потенциальной энергии частицы в этом поле, взятому с обратным знаком.
Пусть на частицу, кроме сил стационарного потенциального поля, действует также неконсервативная сила
Тогда при переходе частицы из точки 1 в точку 2 над ней будет совершаться работа 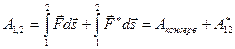 ,где ,где  - работа неконсервативной силы. - работа неконсервативной силы.
Работа консервативных сил равна убыли потенциальной энергии. Тогда:
Суммарная работа всех приложенных к частице сил идет на приращение ее кинетической энергии:
- работа неконсервативных сил затрачивается на приращение полной механической энергии частицы. Потенциальная энергия, как и потенциальная функция, определяется с точностью до произвольной аддитивной постоянной. Однако, это не имеет значения, так как во все функции входит либо разность значений потенциальной энергии, либо ее производные. В каждой конкретной задаче выбирается начало отсчета потенциальной энергии, от которого ведут расчет энергии в других положениях. Поэтому Конкретный вид функции В поле тяжести Рассмотрим систему, состоящую из Каждая из частиц обладает кинетической
Просуммировав эти выражения для всех частиц, получаем:
- полная механическая энергия системы невзаимодействующих частиц, на которые действуют только консервативные силы, остается постоянной.
|

 . (4.11)
. (4.11)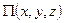 к функции
к функции 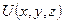 , связанной с
, связанной с 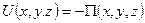 . (4.12)
. (4.12)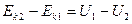 , или
, или 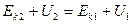 .
.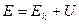 для частицы, находящейся в поле консервативных сил, остается постоянной, т.е. является интегралом движения.
для частицы, находящейся в поле консервативных сил, остается постоянной, т.е. является интегралом движения. , равную сумме кинетической и потенциальной энергии, называют полной механической энергией частицы.
, равную сумме кинетической и потенциальной энергии, называют полной механической энергией частицы.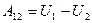
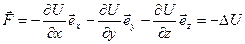
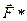 .
.
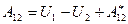 .
.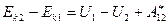 , или
, или 
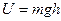 , где
, где 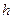 отсчитывается от произвольного уровня.
отсчитывается от произвольного уровня.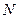 невзаимодействующих между собой частиц, находящихся в поле консервативных сил.
невзаимодействующих между собой частиц, находящихся в поле консервативных сил.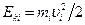 и потенциальной энергией
и потенциальной энергией 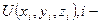 номер частицы, тогда для каждой частицы можно записать:
номер частицы, тогда для каждой частицы можно записать: