Закон сохранения момента импульса.
Уравнения движения частиц имеют вид:
Умножим первое уравнение векторно слева на радиус-вектор первой частицы а второе – на радиус-вектор второй частицы
Ясно, что получаем Внесем массу под знак производной и в векторное произведение,
или Сложив эти уравнения, получаем:
Векторы
Если система замкнутая, правая часть этого соотношения равна нулю, поэтому Мы получили аддитивную сохраняющуюся величину, называемую моментом импульса относительно точки О (рис.4.13). Для отдельно взятой частицы моментом импульса относительно точки О называется псевдовектор Моментом импульса системы относительно точки Оназывается векторная сумма моментов импульсов частиц, входящих в систему: Проекция вектора
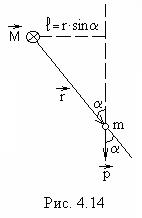
Из рис.4.14 видно, что модуль вектора момента импульса частицы равен
Здесь Рис. 4.14 выполнен в предположении, что точка О, относительно которой берется момент, и вектор Вектор
Рассмотрим два характерных случая. 1. Пусть частица движется по прямой, изображенной на рис.4.15а.
Модуль момента импульса равен 2. Частица движется по окружности радиуса Момент импульса частицы относительно центра окружности О равен по модулю Вектор Плечо постоянно и равно При равномерном движении частицы по окружности момент импульса остается постоянным.
Из рисунка видно, что модуль момента силы равен П роекция вектора
Разложим вектор силы
Если провести окружность радиуса Момент силы
Векторы Момент Тогда момент силы Момент силы характеризует способность силы вращать тело вокруг точки, относительно которой он берется. Е сли тело может вращаться относительно точки О произвольным образом, то под действием силы оно повернется вокруг оси, перпендикулярной к плоскости, в которой лежат сила и точка О, т.е. вокруг оси, совпадающей с направлением момента силы относительно данной точки. Момент силы относительно оси Составляющие
Расстояние Суммарный момент образующих пару сил равен
Учтем, что
где Это выражение не зависит от выбора точки О, т.е. момент пары сил относительно любой точки один и тот же. Вектор момента пары сил перпендикулярен к плоскости, в которой лежат силы, и численно равен произведению модуля одной из сил на плечо. Силы взаимодействия между частицами направлены противоположно вдоль одной и той же прямой (рис.4.18). Их моменты относительно произвольной точки О равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю: В соответствии с определениями моментов импульса и силы и с учетом сказанного выше, уравнение (4.20) можно переписать в виде Из этой формулы следует, что скорость изменения момента импульса механической системы равна моменту внешних сил, приложенных к этой системе. При отсутствии момента внешних сил (в случае замкнутой системы) момент импульса сохраняется. В этом состоит содержание закона сохранения импульса.
|

 Рассмотрим систему, состоящую из двух взаимодействующих частиц, на которые действуют внешние силы (рис.4.13).
Рассмотрим систему, состоящую из двух взаимодействующих частиц, на которые действуют внешние силы (рис.4.13).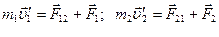 .
.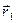 ,
,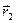 :
: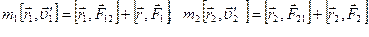 .
. , тогда учитывая, что
, тогда учитывая, что  ,
,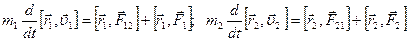 .
.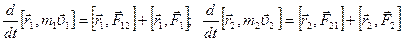
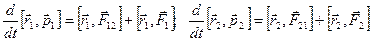
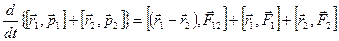 . (4.20)
. (4.20)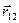 и
и 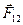 коллинеарны, их векторное произведение равно нулю. Тогда
коллинеарны, их векторное произведение равно нулю. Тогда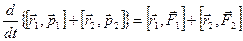
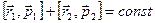 .
.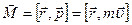 .
.
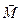 на некоторую ось
на некоторую ось 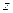 называется моментом импульса частицы относительно этой оси
называется моментом импульса частицы относительно этой оси 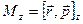 .
. Аналогично, моментом импульса системы относительно оси
Аналогично, моментом импульса системы относительно оси 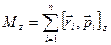 .
. .
. - длина перпендикуляра, опущенного из точки О на прямую, вдоль которой направлен импульс частицы. Эта длина называется плечом импульса относительно точки О.
- длина перпендикуляра, опущенного из точки О на прямую, вдоль которой направлен импульс частицы. Эта длина называется плечом импульса относительно точки О.
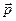 лежат в плоскости рисунка.
лежат в плоскости рисунка. В этом случае момент импульса частицы может изменяться только по величине.
В этом случае момент импульса частицы может изменяться только по величине.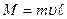 , плечо
, плечо 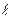 остается неизменным.
остается неизменным.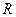 (рис.4.15 б).
(рис.4.15 б).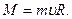
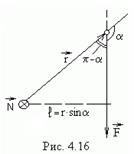 Псевдовектор
Псевдовектор 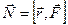 называется моментом силы
называется моментом силы 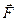 относительно точки О, из которой проводится радиус-вектор
относительно точки О, из которой проводится радиус-вектор  точки приложения силы (рис.4.16).
точки приложения силы (рис.4.16).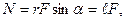 где
где 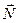 на некоторую ось
на некоторую ось 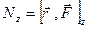
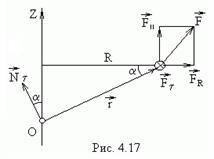
 - параллельную оси
- параллельную оси 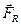 - перпендикулярную к оси
- перпендикулярную к оси 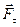 - перпендикулярную к плоскости, проходящей через ось и точку приложения силы (эта составляющая обозначена кружочком с крестиком на рис.4.17).
- перпендикулярную к плоскости, проходящей через ось и точку приложения силы (эта составляющая обозначена кружочком с крестиком на рис.4.17).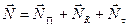 .
.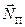 и
и 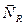 перпендикулярны к оси
перпендикулярны к оси 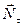 имеет модуль
имеет модуль 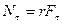 и образует с осью
и образует с осью 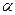 , причем
, причем 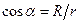 .
.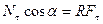 , и момент силы
, и момент силы 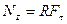 .
.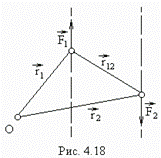 Две равные по величине противоположно направленные силы, не действующие вдоль одной прямой, называются парой сил (рис.4.18).
Две равные по величине противоположно направленные силы, не действующие вдоль одной прямой, называются парой сил (рис.4.18). между прямыми, вдоль которых действуют силы, называется плечом пары.
между прямыми, вдоль которых действуют силы, называется плечом пары.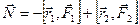 .
. , получаем
, получаем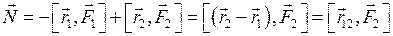 ,
,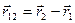 - вектор, проведенный из точки приложения силы
- вектор, проведенный из точки приложения силы 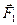 в точку приложения силы
в точку приложения силы  .
.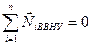 .
.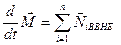 .
.


