Закон сохранения энергииСведем вместе результаты, полученные в предыдущих параграфах. Рассмотрим систему, состоящую из Частицы взаимодействуют друг с другом силами Ранее было установлено, что такие силы являются консервативными, и работа, совершаемая этими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть, кроме внутренних сил, на Уравнение движения для Умножив это уравнение на
Левая часть этого выражения представляет собой приращение кинетической энергии системы: Первое слагаемое правой части равно убыли потенциальной энергии взаимодействия, как следует из выражения (4.14):
Второе слагаемое равно убыли потенциальной энергии системы во внешнем поле консервативных сил:
Последнее слагаемое представляет собой работу внешних неконсервативных сил
Окончательно получаем: Величина
· Если на систему не действуют внешние неконсервативные силы, то полная механическая энергия сохраняется. Это закон сохранения механической энергии . · Для замкнутой механической системы этот закон формулируется следующим образом: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной. · Если в замкнутой системе, кроме консервативных, действуют неконсервативные силы, то полная механическая энергия не сохраняется, и ее изменение равно работе неконсервативных сил: Проинтегрировав, получаем: В этом случае механическая энергия переходит в другие виды энергии, и выполняется более общий закон сохранения всех видов энергии.
|
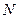частиц с массами 
.
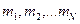, модули которых зависят только от расстояния 
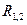между частицами.
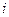-ю частицу действует внешняя консервативная сила 
и внешняя неконсервативная сила 
.
.
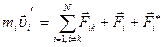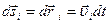и сложив вместе все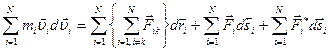 
.
.
.
.
.
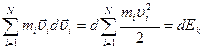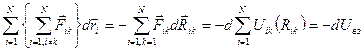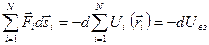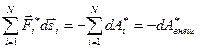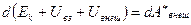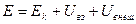есть полная механическая энергия системы.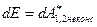
.
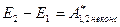