Потенциальная энергия взаимодействия.
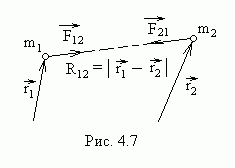
Рассмотрим замкнутую систему, состоящую из двух взаимодействующих частиц (рис.4.7).
Будем считать, что силы взаимодействия частиц
По третьему закону Ньютона Уравнения движения частиц Умножим первое уравнение на
Левая часть этого выражения представляет собой приращение кинетической энергии системы за время
Подставив в это выражение формулу (4.13), получаем Из рис.4.7 видно, что скалярное произведение Тогда Выражение
Следовательно,
Функция · зависит от расстояния между частицами. ·
работа внутренних сил Т.е. не зависит от путей, по которым перемещались частицы, а определяется только начальными и конечными расстояниями между частицами. Таким образом, силы взаимодействия вида (4.13) являются консервативными.
|

 Введем вектор
Введем вектор  , где
, где 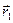 и
и  - радиус-векторы частиц. Расстояние между частицами равно модулю этого вектора.
- радиус-векторы частиц. Расстояние между частицами равно модулю этого вектора.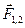 и
и 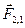 зависят только от расстояния
зависят только от расстояния 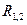 между ними, и направлены вдоль прямой, соединяющей частицы:
между ними, и направлены вдоль прямой, соединяющей частицы: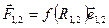 , (4.13)
, (4.13) где
где  - некоторая функция
- некоторая функция 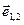 - орт вектора
- орт вектора 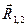 (рис.4.8).
(рис.4.8). .
.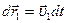 , второе – на
, второе – на  и сложим:
и сложим: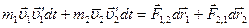 . (4.14)
. (4.14)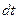 , а правая часть – работу внутренних сил за то же время:
, а правая часть – работу внутренних сил за то же время: .
.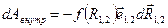 .
. равно приращению расстояния между частицами.
равно приращению расстояния между частицами.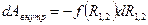 .
. есть приращение некоторой функции от
есть приращение некоторой функции от 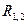 :
: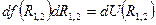 .
.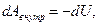 и выражение (4.14) можно представить в виде:
и выражение (4.14) можно представить в виде: .
.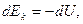 или
или  таким образом, величина
таким образом, величина 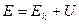 для замкнутой системы сохраняется.
для замкнутой системы сохраняется.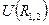 представляет собой потенциальную энергию взаимодействия. Она
представляет собой потенциальную энергию взаимодействия. Она



