Математическая модель межотраслевого баланса
При построении математической модели вводятся следующие обозначения:
Уравнение баланса сводится к равенству объема выпуска каждого производящего сектора сумме потребления его продукции всеми производящими отраслями и сектором народного потребления:
или, в более развернутом виде:
Для реализации расчетов уравнения (6.3)–(6.4) обычно представляют в матричной форме. При этом приняты следующие обозначения: X – вектор выпуска продукции; Y – вектор народного потребления; А – структурная матрица; Е – единичная матрица, которая имеет вид:
Тогда уравнение баланса выражается в виде:
Уравнение (6.5) является основой для решения многих задач, связанных с анализом и планированием экономики. Основными такими задачами являются: – при известной структурной матрице (А) и объемах выпуска (Х) можно определить объемы продукции, идущие на удовлетворение спроса (Y). – при заданном спросе на продукцию (Y) определить объемы выпуска (Х). Первая задача сводится к простому вычислению вектора Y по уравнению (6.5). Решается она путем прямого перемножения матриц (E–A) и X. Для решения второй задачи используется стандартный метод преобразования матричных уравнений: – обе части уравнения (6.5) умножаются матрицу, обратную матрице (Е–А):
Перемножение прямой и обратной матриц дает единичную. Поэтому уравнение (6.6) приобретает вид:
Уравнение (6.7) имеет решение только в том случае, если матрица (Е–А) обратима. Кроме того, исходя из физического смысла, все компоненты вектора Х должны быть больше нуля. Для этого необходимо выполнение условий Хаукинса–Саймона, состоящее в неотрицательности определителей:
Если все определители системы (6.8) больше нуля, то существующая экономическая система может удовлетворить вектор спроса.
Пример Пусть экономика характеризуется структурной матрицей, приведенной в табл. 6.4.
Таблица 6.4
Определить объемы производства каждой отрасли, если народное потребление продукции этих отраслей равно: -промышленная продукция – 30 ден. ед.; -сельскохозяйственное производство – 50 ден. ед.; -энергетика – 20 ден. ед. Для начала решения разместим исходные данные следующим образом:
В соответствии с принятыми в разделе 2 обозначениями присвоим: – ячейкам C5:E7 имя «А»; – ячейкам H5:H7 имя «Y»; – ячейкам C9:E11 имя «E». В соответствии с уравнением (6.5) поэтапно вычислим необходимые матрицы.
Для вычисления матрицы (Е–А). 1. В C13 вводится формула =E–A. 2. Выделяются ячейки C13:E15. 3.Нажимается клавиша F2 и затем выполняется нажатие Ctrl+Shift+Enter. 4. Ячейкам C13:E15 присваивается имя «ЕА»; Для вычисления обратной матрицы (E– A)–1 1. В C17 вызывается стандартная функция =МОБР(EА); 2. Выделяются ячейки C17:E19; 3. Нажимается клавиша F2 и выполняется нажатие Ctrl+Shift+Enter; 4. Ячейкам C17:E19 присваивается имя «ЕАобр»; Для вычисления матрицы X. 1. В C21 вызывается стандартная функция =МУМНОЖ(ЕАобр;Y); 2. Выделяются ячейки C21:С23; 3. Нажимается клавиша F2 и выполняется нажатие Ctrl+Shift+Enter; В ячейках G13–G15 выполнение условий Хаукинса–Саймона. 1. В ячейку G13 формула =МОПРЕД(C13:E15); 2. В ячейку G14 формула =МОПРЕД(C13:D14); 3. В ячейку G15 формула =МОПРЕД(C13). Все определители положительны. Поэтому рассматриваемая экономическая системы в состоянии удовлетворить заданный спрос.
Варианты заданий 1. Для экономики со структурной матрицей, приведенной в табл. 6.4, даны следующие объемы производства по отраслям:
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
2. Дана экономика со следующими объемами производства и собственного потребления (в отсутствие народного потребления):
Определить объемы производства каждой отрасли, необходимые для удовлетворения следующих объемов народного потребления:
3. Дана экономика со следующей структурной матрицей:
И даны следующие объемы производства по отраслям:
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
4. Дана экономика со следующими объемами производства и собственного потребления (в отсутствие народного потребления):
Определить объемы производства каждой отрасли, необходимые для удовлетворения следующих объемов народного потребления:
5. Даны две экономики со следующими структурными матрицами:
Экономика 1
Экономика 2
И даны объемы народного потребления, которые эти экономики должны удовлетворить:
Определить, которая из экономик эффективнее. Указание Эффективность экономик рассчитывается как отношение объемов потребления к общему объему производства по всем отраслям.
6. Даны две экономики со следующими объемами производства и собственного потребления:
Экономика 1
Экономика 2
И даны объемы народного потребления, которые эти экономики должны удовлетворить:
Определить, которая из экономик эффективнее. Указание Эффективность экономик рассчитывается как отношение объемов потребления к общему объему производства по всем отраслям.
7. Для экономики со структурной матрицей, приведенной в табл. 6.4, даны следующие объемы производства по отраслям:
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
8. Дана экономика со следующими объемами производства и собственного потребления (в отсутствие народного потребления):
Определить объемы производства каждой отрасли, необходимые для удовлетворения следующих объемов народного потребления:
9. Дана экономика со следующей структурной матрицей:
И даны следующие объемы производства по отраслям:
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
10. Дана экономика со следующими объемами производства и собственного потребления (в отсутствие народного потребления):
Определить объемы производства каждой отрасли, необходимые для удовлетворения следующих объемов народного потребления:
11. Даны две экономики со следующими структурными матрицами:
Экономика 1
Экономика 2
И даны объемы народного потребления, которые эти экономики должны удовлетворить:
Определить, которая из экономик эффективнее. Указание Эффективность экономик рассчитывается как отношение объемов потребления к общему объему производства по всем отраслям.
12. Даны две экономики со следующими объемами производства и собственного потребления:
Экономика 1
Экономика 2
И даны объемы народного потребления, которые эти экономики должны удовлетворить:
Определить, которая из экономик эффективнее. Указание Эффективность экономик рассчитывается как отношение объемов потребления к общему объему производства по всем отраслям.
13. Для экономики со структурной матрицей, приведенной в табл. 6.4, даны следующие объемы производства по отраслям:
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
14. Дана экономика со следующими объемами производства и собственного потребления (в отсутствие народного потребления):
Определить объемы производства каждой отрасли, необходимые для удовлетворения следующих объемов народного потребления:
15. Дана экономика со следующей структурной матрицей:
И даны следующие объемы производства по отраслям:
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
6.4. Задача об эквивалентности ставок [1]
|

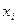 – объем производства в i –ой производящей отрасли;
– объем производства в i –ой производящей отрасли;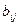 – объем продукции, произведенной в i –ой отрасли и потребляемой в отрасли j;
– объем продукции, произведенной в i –ой отрасли и потребляемой в отрасли j;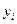 – объем продукции i– ой отрасли, расходуемый на народное потребление;
– объем продукции i– ой отрасли, расходуемый на народное потребление;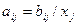 – объем продукции i –ой отрасли, идущий на производство единицы продукции j–ой отрасли. Как указано выше этот параметр называется структурным или технологическим) коэффициентом.
– объем продукции i –ой отрасли, идущий на производство единицы продукции j–ой отрасли. Как указано выше этот параметр называется структурным или технологическим) коэффициентом.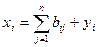 (6.3)
(6.3) . (6.4)
. (6.4)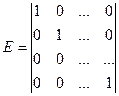 .
.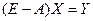 . (6.5)
. (6.5)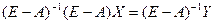 . (6.6)
. (6.6)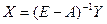 . (6.7)
. (6.7)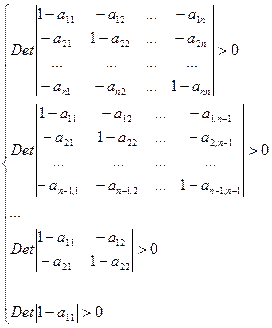 (6.8)
(6.8)


