Последовательность действий при проведении ковариационного ц кросо-спектрального анализов электроэнцефалограмм на ЭВМ типа PC
1. В соответствии о теоремой Котельникова перевести аналоговый ЭЭГ-сигнал в цифровую форму. При этом помнить, что максимальная значащая частота ЭЭГ равняется 30 Гц (следовательно, fквантования ≥ 2fMAX = 60 Гц), а минимальная 0,6 Гц (чтобы получить полный спектр, длина записи T должна быть не менее 2 с).
2. Полученные цифровые последовательности записать в массивы x(t) и y(t) длиной N = T∙ fквантования, при этом N = 2k, где k - целое число.
3. Последовательности x(t) и y(t) дополнить нулями до длины 2N:
4. Из двух действительных последовательностей x*(i) и y*(i) (i=0,…,(2N-1)) составить одну комплексную последовательность z*(i), которую, в свою очередь, разложить на две комплексные последовательности длиной a(i) = z(2i) и b(i) = z(2i+1).
5. Перевести последовательности a(i) и b(i) в частотную область при помощи БПФ:
6. По последовательностям А(k) и B(k) восстановить последовательности Х(k) и У(k), являющиеся частотными отображениями последовательностей x(i) и y(i):
Затем восстанавливаются
* - знак комплексного сопряжения. Необходимо помнить, что Х(k) и У(k) являются комплексными последовательностями. Их модуль вычисляется по формулам:
На практике чаще используются спектры мощности, равные
7. Определить функцию плотности кросс-спектра
Спектры мощности
8. Осуществить обратное преобразование Фурье для функции
Далее определить функцию U*(k), комплексно-сопряженную U(k), и произвести прямое Фурье-преобразование U*(k): u*(t) = БПФ(U*(k)). Затем найти обратное преобразование функции u(y) = (u*(t))* как комплексно-сопряженное к u*(t). Восстановить обратное преобразование Фурье для функции Z(k):
Полученная действительная последовательность z(i) имеет размерность 2N, но в результате добавления в начале алгоритма к исходным последовательностям x(i) и y(i) нулей информативными будут только первые N элементов последовательности. 9. Определить ковариационную функцию
|


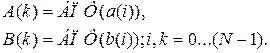



 и
и 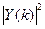 .
.



 при i = 0,…,(N-1). Значения функции вывести на печать.
при i = 0,…,(N-1). Значения функции вывести на печать.


