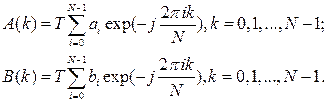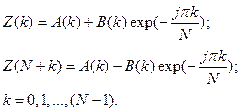ДДФ двойной длины.
Пусть z(i) - комплексная последовательность, i = 0,1,…,(n-1). Преобразуем ее в две другие, вдвое меньшей размерности, следующим образом: a(i) = z(2i); b(i) = z(2i + 1); i = 0,1,…,(n-1). Затем проведем преобразования:
В соответствии с 1-м и 2-м свойствами ДПФ искомую последовательность значений преобразования Фурье получают по формулам
В случае физиологических сигналов действительная и мнимая части последовательности z(i) заполняются двумя действительными последовательностями x(i) и y(i), частотные образы которых затем восстанавливаются в соответствии с 3-м свойством ДПФ.
|