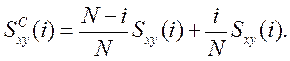Круговая свертка.
Пусть x(nT) и y(nT) имеют ДПФ X(k) и Y(k) соответственно. Если последовательность u(nT) равна круговой свёртке последовательностей x(nT) и y(nT) и
то её ДПФ равно U(k) = X(k)∙Y(k).
Если x(nT) и y(nT) имеют ДПФ X(k) и Y(k) соответственно, то ДПФ последовательности u(nT) = x(nT)y(nT) равно (с точностью до постоянного множителя) круговой свертке Х(k) и Y(k):
Для нас очень важно одно следствие данного свойства: Если x(nT) и y(nT) имеют ДПФ X(k) и Y(k) соответственно, то ДПФ ковариационной последовательности
будет равно где * означает комплексную сопряженность. Последовательность Sxy(k) называется кросс-спектром последовательностей X(k) и Y(k). Обратное ДПФ кросс-спектра дает временную ковариационную функцию
Поскольку для вычисления ковариации во временной области требуется произвести N(N-1)/2 умножений, а в частотной - лишь N/2 (вследствие симметричности спектра), то обычно сначала определяют кросс-спектральную последовательность, а затем находят ее образ во временной области, куда она отображается в вида ковариационной последовательности. Однако следует помнить, что в силу конечности преобразования при обратном ДПФ получается не ковариационная, а круговая ковариационная функция
Для того, чтобы получить истинную ковариационную функцию, исходные последовательности xi, yi, i =0,1,…,(n-1) необходимо дополнить нулями до размерности 2N-1.
|

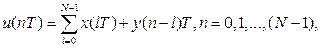
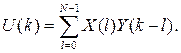
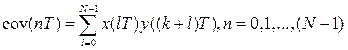
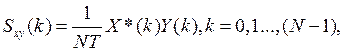

 :
: