Механические характеристики
Моменты М и Мс могут зависеть от времени, от положения, от скорости. Наиболее интересна и важна связь моментов М и Мс со скоростью Поскольку как моменты, так и скорость могут иметь различные знаки, механические характеристики могут располагаться в четырех квадрантах плоскости
Рис. 3. Пример механических характеристик Моменты принято делить на активные и реактивные. Активные моменты могут быть как движущими, так и тормозящими, их направление не зависит от направления движения: момент, созданный электрической машиной (М на рис. 3), момент, созданный грузом, пружиной и т.п. Соответствующие механические характеристики могут располагаться в любом из четырех квадрантов. Реактивные моменты - реакция на движение, они всегда направлены против движения, т.е. всегда тормозящие: момент от сил трения, момент, создаваемый центробежной машиной (Мс на рис. 3) и т.п. Механические характеристики всегда располагаются во втором и четвертом квадрантах. Механические характеристики принято оценивать их жесткостью
Рис. 4. Механические характеристики с различной жесткостью Механические характеристики двигателя и нагрузки, рассматриваемые совместно, позволяют очень просто определить координаты - скорость и моменты - в установившемся (статическом) режиме w уст и Муст. Действительно, если отразить зеркально относительно оси скорости характеристику Мс (рис. 5,а), то точка А пересечения отраженной кривой - Мс с характеристикой двигателя М определит установившийся режим, поскольку выполнится условие М+(-Мс)= 0 или
а) б) Рис. 5. К определению установившегося режима Легко видеть, что здесь мы выполнили одну операцию - перенесли Мс из второго квадранта в первый. Эту операцию можно исключить, если записывать уравнение движения (1) в виде:
где знак “-” перед Механические характеристики двигателя и нагрузки позволяют определить, будет ли статически устойчив установившийся режим, т.е. вернется ли система после действия любого случайного возмущения к исходному статическому состоянию - рис. 6,а, или не вернется - рис. 6,б.
а) б) Рис. 6. К определению статической устойчивости В первом случае (рис. 6,а) показано, что любое случайное, например снижение скорости (w 1 < w уст) сопровождается преобладанием движущего момента М над тормозящимМс, и равновесие восстанавливается, система возвращается в исходное состояние. Во втором случае (рис. 6,б) такое же случайное изменение скорости приводит к преобладанию тормозящего момента, и равновесие не восстанавливается - система статически неустойчива. 2. Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м². Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
|

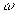 . Зависимости
. Зависимости  и
и 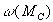 называют механическими характеристиками соответственно двигателя и нагрузки (механизма). Механические характеристики будут служить очень удобным и полезным инструментом при анализе статических и динамических режимов электропривода.
называют механическими характеристиками соответственно двигателя и нагрузки (механизма). Механические характеристики будут служить очень удобным и полезным инструментом при анализе статических и динамических режимов электропривода.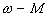 . На рис. 3 в качестве примера показаны характеристики асинхронного двигателя (М) и центробежной машины (Мс). Знаки величин определяют, приняв одно из направлений движения за положительное, например: по часовой стрелке- + или вверх- + и т.п. Моменты, направленные по движению (движущие), имеют знак, совпадающий со знаком скорости(участок w 0 - Мк.з характеристики двигателя); моменты, направленные против движения (тормозящие), имеют знак, противоположный знаку скорости (остальные участки характеристик).
. На рис. 3 в качестве примера показаны характеристики асинхронного двигателя (М) и центробежной машины (Мс). Знаки величин определяют, приняв одно из направлений движения за положительное, например: по часовой стрелке- + или вверх- + и т.п. Моменты, направленные по движению (движущие), имеют знак, совпадающий со знаком скорости(участок w 0 - Мк.з характеристики двигателя); моменты, направленные против движения (тормозящие), имеют знак, противоположный знаку скорости (остальные участки характеристик).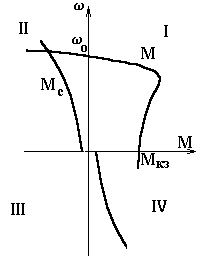
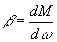 . Они бывают (рис. 4) абсолютно жесткими
. Они бывают (рис. 4) абсолютно жесткими 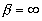 (1), абсолютно мягкими
(1), абсолютно мягкими 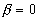 (2) могут иметь отрицательную
(2) могут иметь отрицательную 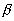 < 0 (3) или положительную (4) жесткость.
< 0 (3) или положительную (4) жесткость.
 , отрезки АВ и ВС будут равными.
, отрезки АВ и ВС будут равными.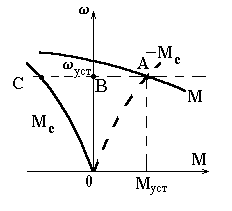

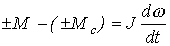 , (4)
, (4)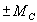 и означает зеркальный перенос характеристики нагрузки (рис. 5,б). Этот прием традиционно используется в электроприводе, т.е. вместо общей и, конечно, правильной общей записи (1) используют измененную форму (4), помня, что это лишь удобный прием, при котором установившийся режим получается при простом пересечении характеристики М и -Мс
и означает зеркальный перенос характеристики нагрузки (рис. 5,б). Этот прием традиционно используется в электроприводе, т.е. вместо общей и, конечно, правильной общей записи (1) используют измененную форму (4), помня, что это лишь удобный прием, при котором установившийся режим получается при простом пересечении характеристики М и -Мс



