ПОСТРОЕНИЯ УГЛОВЫХ СУММ
Синтезирование плоских волн путем суммирования амплитуд в области выносов вдоль наклонных лучей обычно выполняется в два шага. Сначала к данным применяется поправка за линейное приращение (LMO) путем преобразования координат (Claerbout, 1978):
где p - параметр луча, х - вынос, t - полное время пробега, t - линейно смещенное время. После применения поправки за линейное приращение отражение, наклонное на входе, становится горизонтальным. Далее, данные суммируются по оси выносов для получения:
Здесь S(p, t) представляет плоскую волну с параметром луча p = sinq/ v. Повторяя операцию ввода поправки за линейное приращение для различных величин p и суммирование [ур.(7.5)], можно построить полную выборку угловых сумм (или p -выборку), которая включает все составляющие наклона в первоначальных данных.
Угловая сумма и разложение волнового поля на плосковолновые составляющие не различаются между собой. Treitel и др. (1982) выполнил математический анализ процесса разложения на плосковолновые составляющие и сделал различие между общепринятой угловой суммой, рассмотренной здесь, и угловой суммой в собственном смысле. Общепринятая угловая сумма дает точное разложение на плосковолновые составляющие, когда мы имеем дело с линейными источниками; угловая сумма в собственном смысле дает точное разложение на плосковолновые составляющие, когда мы имеем дело с точечными источниками. Угловая сумма в собственном смысле формируется с использованием тех же шагов, которые рассмотрены для общепринятой угловой суммы; исключением является то, что свертка линейно смещенного волнового поля с оператором фильтра выполняется перед суммированием. Этот оператор вносит поправки за трехмерные эффекты, преобразуя волновое поле, полученное по точечному источнику, в волновое поле, полученное по линейному источнику. Пока дело касается кинематики, два типа углового суммирования являются эквивалентными. Они различаются только при обработке амплитуд (Treitel, персональное сообщение). Схематическое описание распределения плоской волны с помощью ур.(7.4) и (7.5) показано на рис.7-9. Начнем с суммирования амплитуд в области удалений взрыв-прибор по горизонтальной траектории, p = 0. Эта линия пересекает годограф отраженной волны в окрестности точки А (вершины). Точка А попадает в точку А` на плоскости (p, t). При наклоне линии суммирования пересечение с годографом происходит в точке В, которая попадает в точку В`. Основной вклад в сумму вдоль наклонной траектории поступает в область точки касания В. Эта область называется зоной Френеля. Чем выше скорость и глубже отражения, тем шире зона Френеля. Фактически суммирование в ур.(7.5) может быть ограничено зоной Френеля. Траектория суммирования характеризуется небольшим наклоном: это p = 1/ v, т.е. асимптота гиперболы. Такая траектория соответствует лучам, отклоняющимся от вертикали на 90 град. Энергия вдоль асимптоты попадает в С` на оси p. При использовании описанного выше распределения гиперболические траектории в области (x, t) становятся эллиптическими траекториями в области (p, t) (Schultz и Claerbout, 1978; см. упр.7.1). В реальных условиях мы никогда не регистрируем годограф бесконечной протяженности и трассу с нулевым выносом. Следовательно, эллиптическая траектория в области наклонного суммирования никогда не бывает полной от A` до С`. На рис.7.10 показан более сложный случай. Докритические отражения А и D (т.е. отражения с углом падения меньше критического) попадают в область пониженных значений p, тогда как закритические отражения С попадают в область повышенных значений p. В идеальном случае линейное отражение в области удаления взрыв-прибор, такое как вступление преломленной волны В, становится точкой в области угловой суммы. И наоборот, линейное отражение в области угловой суммы становится точкой в области удаления взрыв-прибор (упр.7.2).
На рис.7.11 показан пример полевых данных, содержащих, в основном, отражения от дна и многократные отражения в тонком слое. Кроме отражений от дна W имеются два хорошо различимых отражения Р1 и Р2. Кратные отражения распределяются вдоль эллиптических траекторий, сходящихся при p = (1/1500)с/м (величина, обратная скорости в воде). Пример полевых данных, содержащих линейные отражения, показан на рис.7.12. Обратите внимание на интенсивные амплитуды на выборке угловых сумм, которые соответствуют канальным волнам, наблюдаемых в данных выноса. В обоих примерах полевых данных выборки угловых сумм были созданы с использованием только положительных величин p. Следовательно, энергия, рассеянная в обратном направлении в данных выноса на рис.7.12, не представлена в выборке угловых сумм. Перейдем к взаимосвязям между различными областями, которые используются в обработке сейсмических данных. Рассмотрим отражение от наклонной границы в ограниченной полосе пропускания в области выносов (t, x), как показано на рис.7.13. Величина выноса изменяется от 250 до 5000м при шаге между трассами 50м. Это отражение распределяется вдоль хорошо различимой радиальной линии в f-k -области (w, kx). Наклон радиальной линии связан с горизонтальной фазовой скоростью соотношением:
Подставим p = sinq/ v, чтобы найти взаимосвязь между переменными в области преобразования:
На рис.7.13 также показано распределение отражения от наклонной границы в области угловой суммы. Одномерное преобразование Фурье трасс угловой суммы в направлении времени дает амплитудный спектр (p, w), который также показан на рис.7.13. Эта плоскость описывает зависимость горизонтальной фазовой скорости от частоты и используется при анализе канальных волн (Раздел 7.3). Энергия вдоль радиального направления АА` на плоскости (w, kx) эквивалентна энергии вдоль вертикального направления ВВ` на плоскости (p, w).
На рис.7.14 показана пространственно неоднозначная составляющая наклона. Циклический возврат (wraparound), наблюдаемый в плоскости (w, kx), является результатом неадекватной пространственной дискретизации сигнала. Обратите внимание, что составляющие с пространственной неоднозначностью и без нее (участки соответственно 1 и 2) попадают на одну p -трассу. Мы ожидаем, что пространственно неоднозначная часть попадет на ряд отрицательных p -трасс. Однако, диапазон частот с побочной составляющей (21-42Гц) будет отсутствовать на плоскости (p, w), в которую были включены только положительные величины p. На рис.7.14 показан случай одного наклона; восстановление диапазона наклонов рассмотрено на рис.7.17. После выполнения определенного процесса в области наклонных сумм используется обратное распределение для восстановления данных в области выносов. Thorson (1978) предоставил детали процедуры восстановления. Для надлежащего восстановления амплитуд перед обратным распределением применяется ро-фильтрация. Это выполняется путем умножения амплитудного спектра каждой трассы угловой суммы на абсолютную величину частоты. Данное действие, в некоторой степени, аналогично дифференцированию волнового поля перед суммированием, которое включено в интегральную формулировку миграции [ур.(4.5)]. На рис.7.15 показана блок-схема обработки наклонной суммы.
Двумерный амплитудный спектр показывает, что частоты более 48Гц являются пространственно неоднозначными (рис.7.17b).Эта выборка может быть распределена в область угловых сумм (рис.7.17с) и восстановлена с применением меньшего интервала между трассами (рис.7.17d). Первоначальный интервал равен 25м; в восстановленной выборке он составляет 12.5м. Двумерный амплитудный спектр выборки с интерполяцией между трассами показывает отсутствие пространственно неоднозначных частот (рис.7.17е). Тем не менее, обратите внимание на пропущенную высокочастотную энергию при превышении 60Гц. Эта энергия в основном распределена вдоль годографа прямой волны во входной выборке (рис.7.17а) и отсутствует в выходной выборке (рис.7.17d). Мы видим, что восстановление может быть успешным даже для пространственно неоднозначных данных при условии изменения углов наклона в узких пределах.
|

 P (x, t + px)
P (x, t + px)
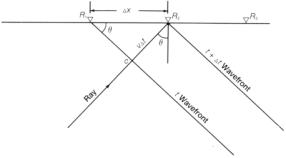
 Рис.7.6 Если параметр луча p определен, можно построить луч в горизонтально-слоистой модели разреза с известной скоростной функцией
Рис.7.6 Если параметр луча p определен, можно построить луч в горизонтально-слоистой модели разреза с известной скоростной функцией
 Рис.7.7 Некоторые лучи для данной величины p, соответствующей одной трассе в плоскости (p, t)
Рис.7.7 Некоторые лучи для данной величины p, соответствующей одной трассе в плоскости (p, t)
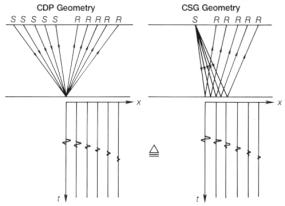 Рис.7.8 Лучи и времена пробега, ассоциированные с геометрией ОГТ и ОПВ
Рис.7.8 Лучи и времена пробега, ассоциированные с геометрией ОГТ и ОПВ
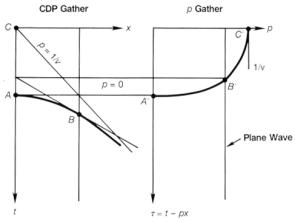 Рис.7.9 Гипербола на выборке ОГТ становится эллипсом на p-выборке
Рис.7.9 Гипербола на выборке ОГТ становится эллипсом на p-выборке
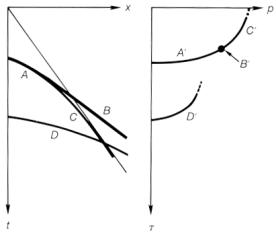 Рис.7-10 Различные вступления на выборке ОГТ распределяются в соответствующую p-выборку. Отражения A,B,C,D распределяются в A`,B`,C`,D`
Рис.7-10 Различные вступления на выборке ОГТ распределяются в соответствующую p-выборку. Отражения A,B,C,D распределяются в A`,B`,C`,D`
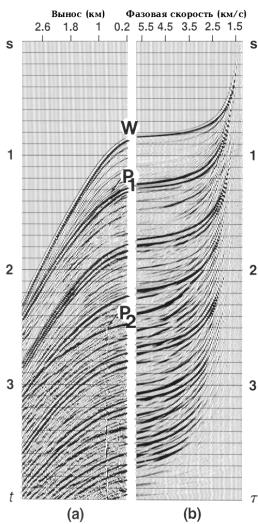 Рис.7.11 (а) Выборка ОПВ, содержащая интенсивные кратные волны; (b) соответствующая p-выборка. Горизонтальная ось в b представляет собой горизонтальную фазовую скорость (1/ p). (Данные Shell и Esso).
Рис.7.11 (а) Выборка ОПВ, содержащая интенсивные кратные волны; (b) соответствующая p-выборка. Горизонтальная ось в b представляет собой горизонтальную фазовую скорость (1/ p). (Данные Shell и Esso).
 Рис.7.13 Одно отражение от наклонной границы в различных областях.
Рис.7.13 Одно отражение от наклонной границы в различных областях.
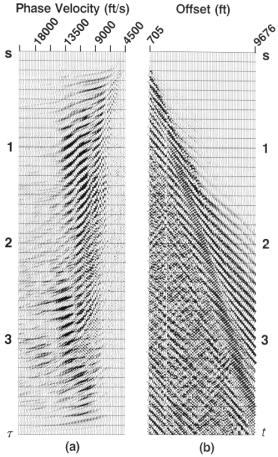 Рис.7.12 (b) Выборка ОПВ; (а) ее угловая сумма. Горизонтальная ось в b представляет собой горизонтальную фазовую скорость (1/ p).
Рис.7.12 (b) Выборка ОПВ; (а) ее угловая сумма. Горизонтальная ось в b представляет собой горизонтальную фазовую скорость (1/ p).
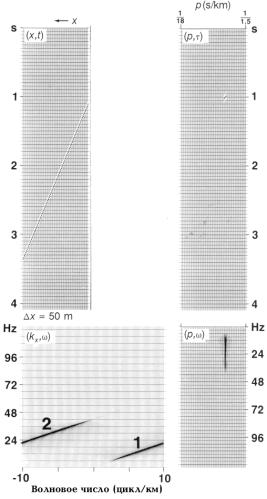 Рис.7.14 Пространственно неоднозначное отражение от наклонной границы в различных областях.
Рис.7.14 Пространственно неоднозначное отражение от наклонной границы в различных областях.




