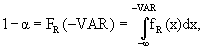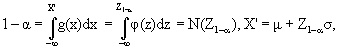Особенности оценки портфеля облигаций

Чаще всего инвесторы вкладывают свои средства не в определенную бумагу, а в разные бумаги, различной доходности и сроком погашения. Это делается с разными целями, чаще всего с целью минимизации рисков путем диверсификации своих вложений. При оценке портфеля облигаций следует учитывать не только доходности бумаг, но и риски. С определением доходности портфеля облигаций проблем не возникает – данный показатель вычисляется на основании средневзвешенной величины (доходности или стоимости), взвешенной по номиналу облигаций в номинальной стоимости всего портфеля. Гораздо сложнее учесть риски. Наиболее распространенной на сегодняшний момент методологией оценивания рыночных рисков является Стоимость Риска (Value-at-Risk, VAR). VAR является суммарной мерой риска, способной производить сравнение риска по различным портфелям (например, по портфелям из акций и облигаций) и по различным финансовым инструментам (например, форварды и опционы).

За последние несколько лет VAR стал одним из самых популярных средств управления и контроля риска в компаниях различного типа. Вызвано это было несколькими причинами. Одной из них стало, несомненно, раскрытие в 1994 г. крупнейшей инвестиционной компанией США Дж.П. Морган системы оценивания риска Riskmetrics^TM и предоставление в свободное пользование базы данных для этой системы для всех участников рынка. Значения VAR, полученные с использованием системы Riskmetrics^TM и до сих пор являются неким эталоном для оценок VAR. Вторая причина заключается в инвестиционном "климате", который царил в конце 1990-х годов и был связан с огромными потерями, понесенными финансовыми институтами, в частности, при оперировании на рынках производных ценных бумаг. В нижеприводимой таблице (Таблица 2.6) указаны потери, понесенные некоторыми западными компаниями и даты, на которые они были обнародованы.

Таблица 9.

Дата отчета	Компания	Потери (в млн. –)
2/93	Showa Shell
1/94	Metallgesellschaft
3/94	Askin Capital Management
4/94	Procter & Gamble
6/94	Paine Webber Bond Mutual Fund
8/94	Piper Jaffray
12/94	Orange County CA
2/95	Barings
10/95	Daiwa

Третьей причиной, является решение организаций, осуществляющих надзор за банками, использовать величины VAR для определения резервов капитала (об этом подробнее см. ниже).

Говоря простым языком, вычисление величины VAR проводится с целью заключения утверждения подобного типа: "Мы уверены на X % (с вероятностью X %), что наши потери не превысят Y долларов в течение следующих N дней". В данном предложении неизвестная величина Y и есть VAR. Она является функцией 2-х параметров: N – временного горизонта и X – доверительного уровня. Так, например, стандартом для брокерско-дилерских отчетов по операциям с внебиржевыми производными инструментами, передаваемым в Комиссию по биржам и ценным бумагам США, являются N равное 2-м неделям и X = 99%. The Bank of International Settlements для оценки достаточности банковского капитала установил X = 99% и N равным 10 дней. Компания Дж. П. Морган опубликовывает свои дневные значения VAR при 95%-ном доверительном уровне.

Исторически подход оценки риска, основанный на VAR, впервые был рекомендован Группой Тридцати (The Global Derivatives Study Group, G30) в 1993 г. в исследовании "Derivatives: Practices and Principles". В том же году Европейский Совет в директиве "EEC 6-93" предписал установку резервов капитала для покрытия рыночных рисков с использованием моделей VAR. В 1994 г. The Bank of International Settlements рекомендовал банкам раскрытие своих значений VAR. В 1995 г. Базельский комитет по надзору за банками предложил банкам использовать собственные модели оценки VAR в качестве основы для расчета резервов капитала. Требования к размеру резервного капитала V рассчитывались как максимум двух величин: текущего значения VAR (VAR _t) и среднего VAR за предыдущие 60 дней, умноженного на коэффициент со значением между 3 и 4:

Значение фактора λ зависит от точности однодневного предсказания модели за предыдущие периоды времени. Так, если обозначить через K – число раз, когда однодневные потери превосходили предсказанное значение VAR за последний год (или последние 250 торговых дней), то различают следующие 3 зоны: "зеленая" зона (K меньше или равно 4), "желтая" зона (K в диапазоне от 5 до 9), "красная" зона (K больше или равно 10). Если K лежит в "зеленой" зоне, то λ = 3, если в "желтой" зоне, то 3 ≤ λ ≤ 4, если в "красной" зоне, то λ = 4.

В 1996 г. организации по регулированию банковской деятельности США одобрили предложение Базельского комитета, а Федеральный Резервный Банк США определил двухлетний период для его реализации.

Разработка и внедрение моделей VAR происходит стремительным образом. В инвестиционных компаниях и банках методология VAR может применяться по крайней мере в 4-х направлениях деятельности.

• Внутренний мониторинг рыночных рисков. Институциональные инвесторы могут вычислять и производить мониторинг значений VAR по нескольким уровням: агрегированному портфеля, по классу актива, по эмитенту, по контрагенту, по трейдеру/портфельному менеджеру и т.д. С точки зрения мониторинга точность оценивания величины VAR уходит на второй план поскольку в данном случае важна величина относительного, а не абсолютного значения VAR, т.е. VAR управляющего или VAR портфеля по сравнению с VAR эталонного портфеля, индекса, другого менеджера или того же менеджера в предыдущие моменты времени.
• Внешний мониторинг. VAR позволяет создать представление о рыночном риске портфеля без раскрытия информации о составе портфеля (который может быть довольно запутанным). Кроме того, регулярные отчеты с использованием цифр VAR, предоставляемые начальству, могут служить одним из аргументов того, что риск, который взяли на себя управляющие менеджеры, находится в приемлемых рамках.
• Мониторинг эффективности хеджа. Значения VAR могут использоваться для определения степени того, насколько хеджирующая стратегия выполняет поставленные цели. Менеджер может оценить эффективность хеджа путем сравнения величин VAR портфелей с хеджем и без хеджа. Если, например, разница между этими двумя величинами невелика, то возникает вопрос о целесообразности хеджирования или правильно ли хеджирование применяется.
• "Что-если" анализ возможных трейдов. Методология VAR позволяет дать больше свободы и автономии управляющему персоналу, так как становится возможным сократить всевозможные бюрократические процедуры, связанные с утверждением тех или иных сделок (особенно с производными инструментами). Это достигается через мониторинг транзакций (сделок) с использованием VAR. Например, высшее руководство может просто установить правило для своих брокеров-дилеров подобного рода: "Никакая операция не должна приводить к увеличению значения VAR более чем на X% начального капитала" и после этого не вдаваться впоследствии в подробности каждого конкретного трейда.

Таким образом, компании могут использовать значения VAR для создания отчетов для менеджеров, акционеров и внешних инвесторов, так как VAR позволяет агрегировать всевозможные рыночные риски в одно число, имеющее денежное выражение. С помощью методологии VAR становится возможным вычислить оценки риска различных сегментов рынка и отождествить наиболее рисковые позиции. Оценки VAR могут использоваться для диверсификации капитала, установки лимитов, а также оценки деятельности компании. В некоторых банках оценка операций трейдеров, а также их вознаграждение вычисляется исходя из расчета доходности на единицу VAR.

Нефинансовые корпорации могут использовать технику VAR для оценки рисковости денежных потоков и принятия решений о хеджировании (защите капитала от неблагоприятного движения цен). Так одной из трактовок VAR является количество незастрахованного риска, которое принимает на себя корпорация. Среди первых нефинансовых компаний, начавших применять VAR для оценки рыночного риска, можно отметить американскую компанию Mobil Oil, немецкие компании Veba и Siemens, норвежскую Statoil.

Инвестиционные аналитики используют VAR для оценивания различных проектов. Институциональные инвесторы, такие как пенсионные фонды, используют VAR для расчета рыночных рисков. Так как было отмечено в исследовании New York University Stern School of Business, около 60% пенсионных фондов США используют в своей работе методологию VAR.

Как уже отмечалось, для заданного временного интервала [t,T], где t – текущий момент времени, и доверительного уровня p VAR есть убыток на временном интервале [t,T], который произойдет с вероятностью 1–p.

Приведем простой пример:пусть дневное значение VAR для данного портфеля есть –2 миллиона при 95% доверительном уровне. Такое значение VAR означает, что при отсутствии резких изменений в рыночных условиях однодневный убыток превысит –2 миллиона в 5% случаев (или 1 раз в месяц, если исходить из того, что в месяце 20 рабочих дней).

Говоря математическим языком, VAR = VAR_t,T определяется как верхняя граница одностороннего доверительного интервала:

Probability {R_t(T) < –VAR} = 1 – α;,

где α; есть доверительный уровень, R_t(T) есть ставка роста капитала портфеля на интервале [t,T] при "непрерывном способе начисления процентов":

R_t(T) = log{V(t+T)/V(t)},

где V(t+T) и V(t) есть значения капитала портфеля в моменты времени t+T и t соответственно. Другими словами, V(t+T) = V(t) × exp{R_t(T)}.

Отметим, что R_t(T) является случайной величиной и характеризуется, таким образом, некоторым вероятностным распределением. Значение VAR определяется из распределения приращений портфеля следующим образом:

где F_R(x) = Probability (R ≤ x) есть функция распределения ставки роста портфеля, f_R(x) есть плотность распределения R_t(T).

Традиционными техниками аппроксимации распределения R_t(T) являются:

• параметрический метод;
• моделирование по историческим данным;
• метод Монте-Карло;
• анализ сценариев.

Если изменения капитала портфеля характеризуются параметрическим распределением, то VAR может быть вычислен через параметры этого распределения. Проиллюстрируем параметрический метод расчета VAR на примере портфеля, состоящего из одного актива. Предположим, что распределение доходности актива является нормальным с параметрами μ (среднее) и σ (стандартное отклонение). Тогда задача расчета VAR сводится к нахождению (1–α)%-квантили стандартного нормального распределения Z_1–α:

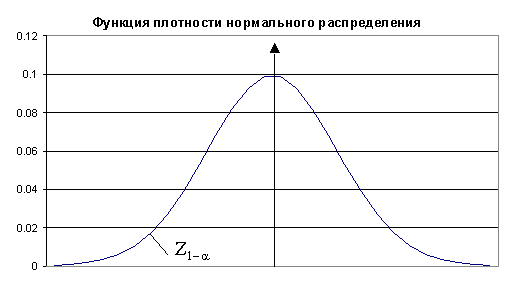
где φ(z) есть плотность стандартного нормального распределения, N(z) есть функция распределения нормального распределения, g(x) есть плотность нормального распределения со средним μ; и стандартным отклонением σ;.

На приводимом ниже рисунке (диаграмма 5) представлена плотность нормального распределения и указана квантиль Z_1–α. Площадь под графиком функции плотности левее Z_1–α (площадь "левого хвоста") равняется 1–α;.

Часто предполагается, что ставка роста актива μ; = 0. Тогда VAR= –V_tZ_1–ασ;, где V_t есть значение капитала портфеля в текущий момент времени t.