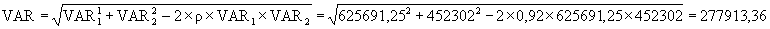Диаграмма 5. Функция плотности нормального распределения
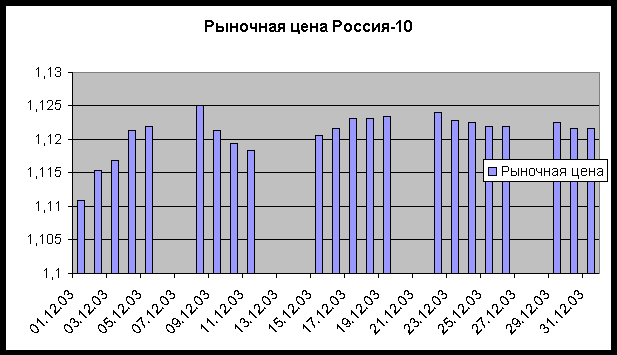
Пример 1: Случай одного актива На следующем графике приведена гистограмма изменений цены Россия-10 за декабрь 2003 года:
Для вычисления VAR воспользуемся тем фактом, что вероятность в "левом хвосте" нормального распределения есть известная функция стандартного отклонения σ, а именно, 5% вероятности нормального распределения находится левее 1,65 стандартных отклонений от среднего значения μ. В данном примере имеем оценки μ = 1,121 (математическое ожидание) и σ = 0,003 (среднеквадратическое отклонение) (см. таблицу 9). Таблица 9. Котировки и параметры бумаг Россия-10 и Россия-30
Все статистические показатели рассчитаны в Excel. При условии, что текущее значение капитала портфеля на 31.12.2003 есть 560,8 млн. рублей, значение VAR на интервале времени 1 месяц при 95%-ном доверительном уровне есть: VAR = 560800 × (1,121 – 1,65 × 0,003) = 625691,25 тыс. руб. Пример 2: Случай двух активов Рассмотрим теперь предыдущий пример портфеля, состоящего из бумаг Россия-10 и Россия-30. Таким образом, значение 1-месячного VAR цены Россия-10 при 95%-ном доверительном уровне есть: VAR = 560800 × (1,121 – 1,65 × 0,003) = 625691,25 тыс. руб. Текущее значение капитала по России-30 на 31.12.2003 есть 480,3 млн. рублей, значение VAR на интервале времени 1 месяц при 95%-ном доверительном уровне есть: VAR = –480,3 × (0,96 – 1,65 × 0,008) = 452302 тыс. руб. Теперь мы в состоянии вычислить суммарный VAR портфеля, используя то, что вариация портфеля из двух активов, имеющих совместное нормальное распределение, равняется сумме вариаций каждого актива и двойной корреляции между этими активами, умноженной на стандартные отклонения активов: (VARportfolio)2 = (VAR1)2 + (VAR2)2 + 2 × ρ × VAR1 × VAR2, где ρ; есть коэффициент корреляции между ценами Россия-10 и Россия-30. Оценкой ρ; является 0,92, т.е. цены Россия-10 и Россия-30 достаточно сильно коррелированны. Таким образом, 1-месячный VAR портфеля при 95%-ном доверительном уровне есть
В приведенных выше примерах нормальное распределение было избрано лишь для иллюстративных целей в силу простоты проводимых вычислений. На практике, как известно, приращения цен активов имеют, как говорят, более тяжелые "хвосты" по сравнению с нормальным законом, т.е. в реальности наблюдается больше "экстремальных" событий по сравнению с тем, что можно было бы ожидать при нормальном распределении. VAR по своей природе, как раз и имеет дело с предсказанием событий из "хвостов" распределения (события "катастрофического риска", хорошо известные в страховом и перестраховочном бизнесе). Поэтому более реалистичным представляется использовать распределения типа Парето, для которого вероятность больших отклонений дается следующим выражением: Probability(R≤x) = FR(x) ≈ ax–α, при x→∞;. Здесь a>0 – константа, а α>0 есть так называемый индекс "хвоста". Метод моделирования по историческим данным состоит в конструировании распределения изменений портфеля Rt(T) по историческим данным. В данном случае делается только одна гипотеза о распределении доходности капитала портфеля: "будущее" будет вести себя также как и "прошлое". Метод Монте-Карло заключается в определении статистических моделей для активов портфеля и их моделировании посредством генерации случайных траекторий. Значение VAR вычисляется из распределения ставок роста капитала портфеля, аналогичного тому, которое изображено на гистограмме для Россия-10, но полученного в результате искусственного моделирования. Метод анализа сценариев изучает эффект изменения капитала портфеля в зависимости от изменения величин рисковых факторов (напр., процентной ставки, волатильности) или параметров модели. Моделирование происходит в соответствии с определенными "сценариями". Так многие банки оценивают величину "PV01" своих портфелей с "фиксированной доходностью" (fixed-income portfolios, т.е. портфелей, состоящих из инструментов "на процентную ставку": облигаций, форвардов на процентную ставку, свопов и т.д.), которая вычисляется как изменение капитала портфеля при параллельном сдвиге кривой доходности на 100 базисных пунктов. К сожалению, ответа на вопрос, какой из методов оценивания VAR является наилучшим, по-видимому, не существует. Использование того или иного метода должно основываться на таких факторах как качество базы данных, простота реализации метода, наличие быстродействующих компьютеров, требования к надежности полученных результатов и т.д. В заключение хотелось бы отметить, что методология VAR не является панацеей от финансовых потерь. Она всего лишь помогает компаниям представить, являются ли риски, которым они подвержены, теми рисками, которые они хотели бы на себя принять или думают, что они на себя приняли. VAR не может сказать управляющему компании "сколько риска нужно взять", а может только сказать "сколько риска уже взято". VAR может и должен использоваться не взамен, а в дополнение к другим методам анализа риска таким, например, как Shortfall-at-Risk (SAR, с редняя величина убытка), когда интересуются не только граничной величиной капитала, ниже которой следует ожидать убыток с определенной долей вероятности, а и размером этого убытка. Итак, мы рассмотрели основные подходы к оценке облигаций, показатели, используемые при этом, а также возможные пути учета различных рисков, как при оценке самой бумаги, так и при оценке портфеля облигаций. В следующей главе рассмотрим альтернативные походы к оценке портфеля облигаций и, кроме того, отдельно выделим облигации с встроенными опционами.
Контрольные вопросы: 1. В чем состоит основная роль рынка ценных бумаг? 2. Назовите функции рынка ценных бумаг 3. В чем принципиальное отличие акций от облигаций? 4. В каких целях проводится финансовый анализ эмитента? 5. В чем принципиальное отличие фундаментального анализа ценных бумаг от технического? 6. Что означает фраза "рынки ценных бумаг эффективны"? Обсудите. 7. Опишите три формы EMH. 8. Обсудите эмпирическую обоснованность EMH. 9. "Можно получить сверхприбыль, инвестируя в акции менее крупных фирм". Прокомментируйте. 10. Обсудите главный смысл EMH для менеджеров в мобилизации финансов. 11. "При определенных условиях "креативный бухучет" может влиять на стоимость фирмы". Прокомментируйте. 12. "Самодельные стратегии инвесторов могут соперничать с некоторыми создающими цену решениями менеджеров". Обсудите.
Раздел 3. ПЕРВИЧНОЕ ПУБЛИЧНОЕ РАЗМЕЩЕНИЕ ЦЕННЫХ БУМАГ (IPO)
|