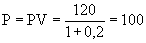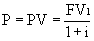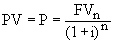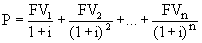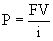РЫНОЧНАЯ СТОИМОСТЬ КАПИТАЛЬНЫХ АКТИВОВ

Капитальный актив – это имущество, приносящее доход. К капитальным активам относятся производственное оборудование, магазин, сдаваемое жилье, участок земли, ценная бумага и т.д. По сути, покупая капитальный актив, люди фактически покупают будущие доходы. Поэтому сегодняшняя цена такого актива будет равна приведенной стоимости этих доходов, определяемой путем дисконтирования.

Следовательно, рыночная стоимость капитального актива (P) зависит от:

• величины приносимых в будущем доходов (FV);
• сроков до получения доходов (n);
• рыночной процентной ставки (i);
• риска неполучения дохода. [Фактор риска в целях упрощения здесь не рассматривается.]

Предположим, капитальный актив – государственная облигация – принесет доход (120 руб.) один единственный раз через год. При этом рыночная процентная ставка составляет 20% годовых. Какую цену согласятся покупатели заплатить за такую облигацию сегодня?

Для ответа на этот вопрос учтем, что у покупателей есть альтернатива: вложить деньги в банк под 20% годовых или в облигацию. Поэтому им не выгодно покупать облигацию дороже, чем за 100 руб. Нет смысла, например, платить 105 руб., чтобы вернуть 120 руб. через год, ибо вложив те же 105 руб. в банк можно через год получить 126 руб. Разумеется, ни один из покупателей не отказался бы от покупки облигации дешевле, чем за 100 руб. Покупка, например, за 90 руб. является в их глазах выгодной сделкой: платим сегодня 90 руб., через год получаем 120 руб., если же вложить эти 90 руб. в банк, то больше 108 руб. получить не удастся.

К огорчению покупателей такой вариант вряд ли пройдет. Даже если некоторые из нынешних владельцев облигаций, остро нуждаясь в деньгах, и согласятся уступить их за бесценок, в условиях конкурентного рынка набежит столько желающих приобрести облигации, что их цена автоматически возрастет. В конечном счете цена данной облигации будет колебаться вокруг 100 руб.:

При такой цене покупателям становится безразлично, куда вкладывать деньги – в банк или в облигацию.

В общем случае сегодняшняя рыночная цена капитального актива, который принесет доход один раз через один год, определяется по формуле:

Именно такую сумму и согласится инвестор заплатить сегодня за данный актив.

Соответственно, если актив принесет доход (FV_n) первый и единственный раз только через n лет, цена актива сегодня составит:

Если актив приносит доход каждый год на протяжении n лет, формула принимает вид:

Если доход, получаемый каждый год постоянен (FV₁ = FV₂ =...= FV_n = FV), а число лет бесконечно велико, формула упрощается: