Погрешности элементарных функций
Таблица 4
Наиболее часто встречаются следующие случаи определения погрешностей: 1. Погрешности в суммах и разностях. Если а1 и а2 измерены с погрешностями Δа1 и Δа2 и измеренные значения используются для вычисления суммы или разности А = а1 ± а2, то суммируются абсолютные погрешности (без учета знака): ΔА = Δа1 + Δа2. 2. Погрешности в произведениях и частных. Если измеренные значения а1 и а2 используются для вычисления А = а1 × а2 или А = а1 / а2, то суммируются относительные погрешности: εА = εа1 + εа2, где ε = Δ а / а. 3. Измеренная величина умножается на точное число. Если а используется для вычисления произведения А = В × а, в котором В не имеет погрешности, то А = | В | × ε а. 4. Возведение в степень. Если а используется для вычисления степени А = аn, то А = n × ε а. 5. Погрешности в произвольной функции одной переменной. Если а используется для вычисления функции А (а), то:
Пример 1. Производится косвенное измерение электрической мощности, рассеиваемой на резисторе сопротивлением R при протекании по нему тока I. Так как P = I 2 × R, то, применяя правила 2 и 4, получим εP = εR + 2εI.
Пример 2. Измерением найдено значение угла α = (20±3)°. Необходимо найти cosα. Наилучшая оценка для cos20° = 0,94. Погрешности Δα = 3° = 0,05 рад. Тогда по правилу 5 имеем εcosα = (sin20°) × 0,05 = 0,34 × 0,05 = 0,02. Окончательно cosα = 0,94 ± 0,02.
|



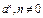
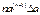




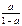
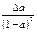
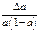
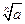

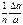
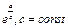
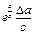
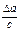
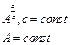
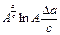

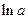



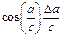
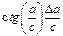


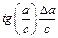
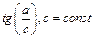
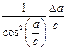


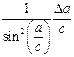
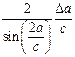
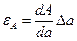 .
.


