Пусть существует функция нескольких переменных f = f (x, y, z …) и пусть существует некоторая точка М 0 с координатами М 0(x 0, y 0, z 0…), в которой эта функция определена. Зафиксируем все переменные, кроме первой: f (x, y 0, z 0…). Тогда предел функции f в точке М 0 равен:
 .
.
Определение. Если данный предел существует и конечен, то он называется частной производной функции f по переменной x, вычисленной в т x 0.
Аналогично определяются частные производные по всем остальным переменным:
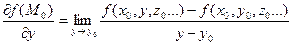 ;
;
 и т.д.
и т.д.
Пример. Вычислить частные производные первого порядка для следующих функций:
а) f =(xy) z; б) f =sin(x 2+ y 2); в) 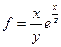 .
.
Решение:
а) найдем сначала частную производную функции по переменной x:  , тогда все остальные переменные (y и z) зафиксируем, т.е. сейчас будем считать их постоянными величинами. Функцию удобно представить в виде произведения: f =(xy) z = xzyz. Тогда:
, тогда все остальные переменные (y и z) зафиксируем, т.е. сейчас будем считать их постоянными величинами. Функцию удобно представить в виде произведения: f =(xy) z = xzyz. Тогда: 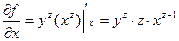 . Мы вынесли yz за знак производной, как постоянную величину, а затем нашли производную по x от оставшейся степенной функции xz.
. Мы вынесли yz за знак производной, как постоянную величину, а затем нашли производную по x от оставшейся степенной функции xz.
Теперь найдем частную производную функции по переменной y:  . Теперь зафиксируем переменные x и z. Аналогично первому случаю, разобьем функцию на сомножители: f =(xy) z = xzyz. Тогда:
. Теперь зафиксируем переменные x и z. Аналогично первому случаю, разобьем функцию на сомножители: f =(xy) z = xzyz. Тогда:  .
.
Наконец, найдем частную производную функции по переменной z:  . Теперь x и y являются фиксированными переменными и функцию f можно рассматривать как функцию вида f =a x. Производная этой функции является табличной и определяется следующим образом:
. Теперь x и y являются фиксированными переменными и функцию f можно рассматривать как функцию вида f =a x. Производная этой функции является табличной и определяется следующим образом: 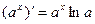 . Для нашей функции это будет выглядеть следующим образом:
. Для нашей функции это будет выглядеть следующим образом: 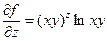 .
.
б) найдем сначала частную производную функции по переменной x:  , тогда переменная y будет фиксированной величиной. Итак:
, тогда переменная y будет фиксированной величиной. Итак:
 . Здесь встретилась сложная функция, и мы сначала нашли производную от внешней функции, а затем от внутренней. При нахождении производной от суммы (x 2+ y 2) помним, что y не меняется и, следовательно, производная от постоянной величины y 2 равна нулю.
. Здесь встретилась сложная функция, и мы сначала нашли производную от внешней функции, а затем от внутренней. При нахождении производной от суммы (x 2+ y 2) помним, что y не меняется и, следовательно, производная от постоянной величины y 2 равна нулю.
Теперь найдем частную производную функции по переменной y:  . Фиксированной будет переменная x. Аналогично предыдущему получим:
. Фиксированной будет переменная x. Аналогично предыдущему получим:
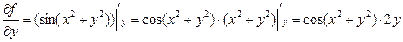 .
.
в) найдем частную производную функции по переменной x:  , тогда y и z – зафиксированные переменные и функцию можно преобразовать следующим образом:
, тогда y и z – зафиксированные переменные и функцию можно преобразовать следующим образом: 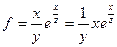 . Постоянную величину
. Постоянную величину 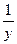 можно вынести за знак производной и искать производную от произведения
можно вынести за знак производной и искать производную от произведения 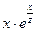 . Воспользовавшись правилом определения производной суммы, получим в скобках два слагаемых, в одном из которых нужно искать производную сложной функции
. Воспользовавшись правилом определения производной суммы, получим в скобках два слагаемых, в одном из которых нужно искать производную сложной функции 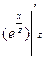 . Получим:
. Получим:

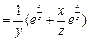 .
.
При определении производной функции по переменной y:  , неизменными считаем x и z. Здесь исходную функцию можно преобразовать так:
, неизменными считаем x и z. Здесь исходную функцию можно преобразовать так: 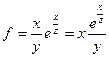 . Мы видим произведение некоторой фиксированной величины (а именно x) на дробь. Теперь для нахождения производной вынесем за знак производной x и воспользуемся правилом для производной дроби:
. Мы видим произведение некоторой фиксированной величины (а именно x) на дробь. Теперь для нахождения производной вынесем за знак производной x и воспользуемся правилом для производной дроби:
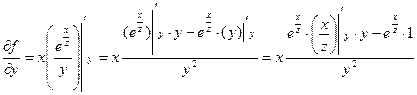
 .
.
Производная  равна нулю, так как сейчас переменные x и z фиксированы, а производная от постоянной величины есть ноль.
равна нулю, так как сейчас переменные x и z фиксированы, а производная от постоянной величины есть ноль.
Теперь найдем производную функции по переменной z:  , постоянными будут величины x и y. Тогда дробь
, постоянными будут величины x и y. Тогда дробь 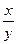 можно вынести за знак производной и искать производную только от
можно вынести за знак производной и искать производную только от 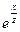 . Получим:
. Получим:
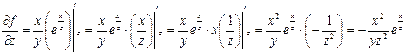 .
.

 .
.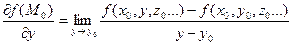 ;
; и т.д.
и т.д.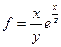 .
. , тогда все остальные переменные (y и z) зафиксируем, т.е. сейчас будем считать их постоянными величинами. Функцию удобно представить в виде произведения: f =(xy) z = xzyz. Тогда:
, тогда все остальные переменные (y и z) зафиксируем, т.е. сейчас будем считать их постоянными величинами. Функцию удобно представить в виде произведения: f =(xy) z = xzyz. Тогда: 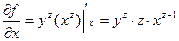 . Мы вынесли yz за знак производной, как постоянную величину, а затем нашли производную по x от оставшейся степенной функции xz.
. Мы вынесли yz за знак производной, как постоянную величину, а затем нашли производную по x от оставшейся степенной функции xz. . Теперь зафиксируем переменные x и z. Аналогично первому случаю, разобьем функцию на сомножители: f =(xy) z = xzyz. Тогда:
. Теперь зафиксируем переменные x и z. Аналогично первому случаю, разобьем функцию на сомножители: f =(xy) z = xzyz. Тогда:  .
. . Теперь x и y являются фиксированными переменными и функцию f можно рассматривать как функцию вида f =a x. Производная этой функции является табличной и определяется следующим образом:
. Теперь x и y являются фиксированными переменными и функцию f можно рассматривать как функцию вида f =a x. Производная этой функции является табличной и определяется следующим образом: 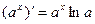 . Для нашей функции это будет выглядеть следующим образом:
. Для нашей функции это будет выглядеть следующим образом: 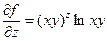 .
. . Здесь встретилась сложная функция, и мы сначала нашли производную от внешней функции, а затем от внутренней. При нахождении производной от суммы (x 2+ y 2) помним, что y не меняется и, следовательно, производная от постоянной величины y 2 равна нулю.
. Здесь встретилась сложная функция, и мы сначала нашли производную от внешней функции, а затем от внутренней. При нахождении производной от суммы (x 2+ y 2) помним, что y не меняется и, следовательно, производная от постоянной величины y 2 равна нулю.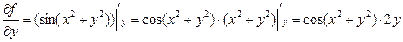 .
.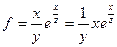 . Постоянную величину
. Постоянную величину 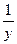 можно вынести за знак производной и искать производную от произведения
можно вынести за знак производной и искать производную от произведения 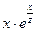 . Воспользовавшись правилом определения производной суммы, получим в скобках два слагаемых, в одном из которых нужно искать производную сложной функции
. Воспользовавшись правилом определения производной суммы, получим в скобках два слагаемых, в одном из которых нужно искать производную сложной функции 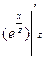 . Получим:
. Получим:
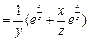 .
.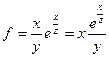 . Мы видим произведение некоторой фиксированной величины (а именно x) на дробь. Теперь для нахождения производной вынесем за знак производной x и воспользуемся правилом для производной дроби:
. Мы видим произведение некоторой фиксированной величины (а именно x) на дробь. Теперь для нахождения производной вынесем за знак производной x и воспользуемся правилом для производной дроби: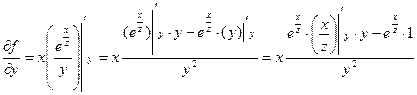
 .
. равна нулю, так как сейчас переменные x и z фиксированы, а производная от постоянной величины есть ноль.
равна нулю, так как сейчас переменные x и z фиксированы, а производная от постоянной величины есть ноль.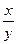 можно вынести за знак производной и искать производную только от
можно вынести за знак производной и искать производную только от 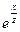 . Получим:
. Получим: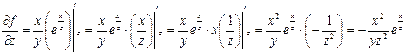 .
.


