Метод наименьших квадратов
Этот метод является одним из наиболее распространенных приемов статистической обработки экспериментальных данных, относящихся к различным функциональным зависимостям физических величин друг от друга. В том числе, он применим к линейной зависимости (2.26), и позволяет получить достоверные оценки ее параметров: коэффициента наклона a и сдвига относительно начала координат b, а также оценить их погрешности. Дело в том, что через одну и ту же совокупность точек на плоскости можно провести различные прямые, причем часть экспериментальных точек на эту прямую не попадает. Задача заключается в отыскании такой прямой, для которой все не попавшие на нее точки отстоят на минимальные расстояния (по сути это абсолютные погрешности измерений). Так как точки будут располагаться по обе стороны от проведенной прямой, то погрешности будут и положительными и отрицательными, и для нахождения их совокупного влияния каждую из них необходимо возвести в квадрат (чтобы избежать компенсации при сложении) и затем сложить. Полученная сумма должна быть минимальной. Рассмотрим статистическую модель эксперимента, в котором исследуют линейную зависимость. Пусть проведено n парных измерений величин x и y: xi, yi, где i = 1,..., n. По экспериментальным данным необходимо найти оценки параметров a и b, а также оценки их дисперсий sa2 и sb2. Для практических расчетов методом наименьших квадратов удобно использовать следующий алгоритм: 1. Вычислить значения следующих средних величин:
2. Определить оптимальные значения коэффициентов а и b:
3. Определить квадрат среднего квадратичного отклонения σ;2:
4.Определить квадраты средних квадратичных отклонений σа 2 и σb 2:
5. Вычислить погрешности Эти выражения удобны и для прямых расчетов на калькуляторе, и для программирования вычислений при использовании компьютера. Многие прикладные компьютерные программы (MathCAD, Excel и др.) содержат метод наименьших квадратов. Часто после введения экспериментальных точек они строят график зависимости и тут же автоматически обрабатывают его для определения оценок параметров и их погрешностей. Контрольные вопросы 1. Что такое измерение? Чем отличаются прямые и косвенные измерения? 2. Какие погрешности называются случайными? систематическими? промахами? Приведите примеры. 3. Расскажите, в какой последовательности производится обработка результатов прямых измерений. 4. Как производятся обработка результатов косвенных измерений? Напишите выражение для абсолютной погрешности, относительной погрешности при обработке результатов косвенных измерений. 5. С каким числом значащих цифр записывается погрешность результата измерений и сам результат? С каким числом значащих цифр достаточно производить вычисления погрешностей? 6. Что такое график? 7. Как выбирают и наносят на график масштаб? 8. Как следует проводить кривую по нанесенным на график экспериментальным точкам? Почему? 9. В чем достоинства графического представления результатов эксперимента? 10. В чем смысл линеаризации экспериментальных зависимостей? Опишите последовательность действий при графической обработке линейной зависимости. 11. Что такое метод парных точек? Как его применить на практике? 12. В чем сущность метода наименьших квадратов? Каков его алгоритм? ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Селиванов, М.Н., Фридман, А.Э., Кудряшова Ж.Ф. Качество измерений. Метрологическая справочная книга. – Л.: Лениздат, 1987. 2. Демкович, В.П., Прайсман Н.Я. Приближенные вычисления в школьном курсе физики. – М.: Просвещение, 1967. 3. Зайдель, А.Н. Элементарные оценки ошибок измерений. Изд. 3-е. – Л.: Наука, 1968. 4. Каменецкий, С.Е. Обработка результатов измерений при выполнении лабораторных работ. – Физика в школе, 1961. – № 1. 5. Поттер, Д. Вычислительные методы в физике. – М.: Наука, 1978. 6. Степанов, С.В., Смирнов А.В. Лабораторный практикум по физике / Под ред. Степанова С.В. – М.: ФОРУМ: ИНФРА-М, 2003. 7. Фетисов, В.А. Оценка точности измерений в курсе физики средней школы. Пособие для учителей. – М.: Просвещение, 1974. 8. Тартаковский, Д.Ф. Метрология, стандартизация и технические средства измерений: Учеб. для вузов. – М.: Высш. шк., 2001. 9. Лабораторные занятия по физике: Учебное пособие / Л.Л. Гольдин, Ф.Ф. Игошин, С.М. Козел и др.: Под ред. Гольдина Л.Л. – М.: Наука. Главная редакция физико-математической литературы, 1983.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Гмурман, В.Е. Элементы приближенных вычислений. – М: Высшая школа, 2005. 2. Колемаев, В.А., Калинина, В.Н. Теория вероятностей и математическая статистика: Учебник / Под ред. Колемаева В.А. – М.: ИНФРА-М, 1999. 3. Сизиков, В. С., Математические методы обработки результатов измерений. – М: Политехника, 2001 год. 4. Кузнецов, В.А., Ялунина, Г.В. Основы метрологии. – М.: Издательство стандартов, 1995. 5. Сысоев С.М. Лабораторный практикум по электричеству и магнетизму: Методические указания к лабораторным работам по курсу общей физики. Для студентов всех специальностей / Сысоев С.М., Манина Е.А., Никонова Н.О.; Под ред. С.М. Сысоева. – Сургут: Изд-во СурГУ, 2004.
|

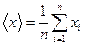 ,
, 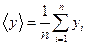 ,
, 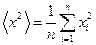 ,
, 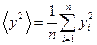 ,
, 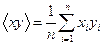 .
.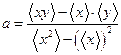 ,
, 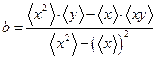 .
.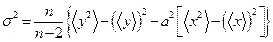 .
.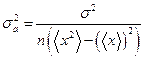 ,
, 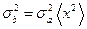 .
.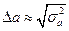 и
и 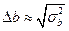 .
.


