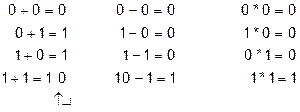С практической точки зрения представляет интерес процедура взаимного преобразования двоичных, восьмеричных и шестнадцатеричных чисел.

 

Правило 2. Для перевода целого двоичного числа в восьмеричное, необходимо разбить его справа налево на группы по три цифры (самая левая группа может содержать менее трех двоичных цифр), затем каждой группе поставить в соответствие ее восьмеричный эквивалент (см. табл.3). Группу из трех двоичных цифр часто называют «двоичной триадой».

Пример: 11011001₂ = 11 011 001₂ = 331_8.

 

Двоичный, восьмеричный и шестнадцатеричный эквиваленты для десятичных чисел от 0 до 15

 

Таблица 3

 

Десятичное число	Двоичное число	Восьмеричное число	Шестнадцатеричное число
			A
			B
			C
			D
			E
			F

 

Правило 3. Перевод целого двоичного числа в шестнадцатеричное производится путем разбиения данного числа на группы по четыре цифры - «двоичные тетрады».

Пример: 1100011011001₂ = 1 1000 1101 1001₂ = 18D9_16.

 

Правило 4. Для перевода дробных частей двоичных чисел в восьмеричную или шестнадцатеричную системы счисления аналогичное разбиение на триады или тетрады производится от точки вправо (с дополнением недостающих цифр нулями).

Примеры: 0,1100011101₂ = 0, 110 001 110 100₂ = 0,6164₈;

0,1100011101₂ = 0, 1100 0111 0100₂ = 0,С74_16.

 

Правило 5. Перевод восьмеричных (шестнадцатеричных) чисел в двоичные, производится обратным путем - сопоставлением каждому знаку числа соответствующей тройки (четверки) двоичных чисел.

Преобразования чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы и обратно столь просты (по сравнению с операциями между этими тремя системами и привычной нам десятичной системой счисления) потому, что числа 8 и 16 являются целыми степенями числа 2 (23; 24). Этой простотой и объясняется популярность восьмеричной и шестнадцатеричной систем счисления в вычислительной технике и программировании.

 

Примеры перевода чисел из одной позиционной системы счисления в другую сведены в таблицу-«подсказку» — схема 7, в которой в сжатой, но информационно-емкой форме представлены способы перевода из одной системы счисления в другую.

 

 

 

Над числами, записанными в любой системе счисления, можно производить различные арифметические операции.

Правила выполнения арифметических действий над двоичными числами определяются арифметическими действиями над одноразрядными двоичными числами.

Сложение Вычитание Умножение

перенос
в старший
разряд

 

Правила выполнения арифметических действий во всех позиционных системах счисления аналогичны.