Погрешности косвенных измерений
Общие правила вычисления погрешностей косвенных измерений выводятся с помощью дифференциального исчисления [4]. Пусть искомая величина z определяется из прямых измерений величины а, причем z = f (a). (22) Тогда
Полагая величину погрешности прямых измерений Δ а,очень малой по сравнению с а, можно для определения погрешности косвенных измерений воспользоваться связью дифференциала функции df с бесконечно малым изменением аргумента
Абсолютную погрешность результата косвенных измерений получим, используя разложение функции f (a) в ряд Тейлора
Отбрасывая члены, содержащие
т. е. абсолютная погрешность вычисления функции одного переменного равна абсолютной погрешности аргумента, умноженной на первую производную этой функции. Относительная погрешность равна
Полагая, что
где знак d после дифференцирования следует заменить на Δ. Т. е. относительная погрешность функции одного переменного равна дифференциалу натурального логарифма этой функции. Пусть измеряемая величина является функцией двух непосредственно измеренных величин
Здесь Напомним, что частная производная функции многих переменных f по одной переменной, например а, является обычной производной функции f по а, причем переменная b считается постоянным параметром. Аналогично для
При оценке точности косвенного результата часто оказывается удобным получить сначала относительную погрешность ε;. Для этого достаточно прологарифмировать, а затем продифференцировать расчетную зависимость
Затем определяется абсолютная погрешность измерения: Универсальных формул для подсчета величины погрешности косвенных измерений не существует. Вид формулы для расчета погрешности будет зависеть от функциональной зависимости, по которой рассчитывается результат косвенного измерения. Эту формулу можно найти, применяя равенство (30)[6].
|

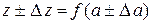 . (23)
. (23)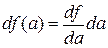 . (24)
. (24) (25)
(25)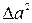 и более высокие степени
и более высокие степени  , получим
, получим (26)
(26) (27)
(27)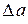 ~ da и
~ da и 
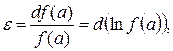
 (28)
(28) . Можно показать [4], что
. Можно показать [4], что . (29)
. (29) и
и  - частные производные функции
- частные производные функции  по переменным а и b соответственно (вычисляются при
по переменным а и b соответственно (вычисляются при 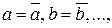 ), а величины
), а величины 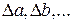 определяют, например, с помощью коэффициентов Стьюдента для одного и того же значения доверительной вероятности α.
определяют, например, с помощью коэффициентов Стьюдента для одного и того же значения доверительной вероятности α.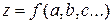 получим
получим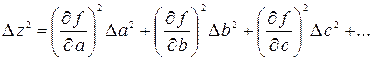 (30)
(30)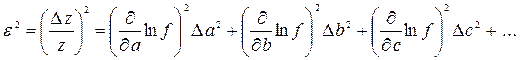 (31)
(31) .
.


