Методом наименьших квадратов
Параметры наилучшей прямой можно определить не только графически, но и аналитически. Наилучшая прямая (32) определяется по правилу «наименьших квадратов», т. е. параметрам а и b приписываются такие значения, при которых величина
имеет минимум[11]. Как известно, функция f (А) принимает минимальное значение при A = A min, если ее первая производная f '(А) = Из условий минимума получаются следующие формулы для нахождения наилучших значений а и b по измеренным значениям хi,yi (i= 1, 2,..., п) [6]:
где
При расчетах следует помнить, что в числителе первой формулы обычно вычитаются близкие по величине члены, что вызывает необходимость удерживать при вычислениях много значащих цифр. Для определения параметра k прямой (35), проходящей через начало координат получается следующая формула:
Формулы для нахождения погрешностей соответствующих параметров a, b, k будут иметь вид:
где
Изложенный выше способ применения метода наименьших квадратов можно обобщить и на некоторые случаи нелинейной зависимости. Например, при изменении температуры T в небольшом интервале
где L – удельная теплота испарения воды, Так как зависимость давления от температуры и теплоты испарения воды является нелинейной, то метод наименьших квадратов следует применять не к самим давлениям, а к логарифмам. Логарифмируя зависимость (43), получим Сравнивая полученное выражение с формулой для линейной зависимости (32), видим, что Формулы (38) запишутся следующим образом:
Следует, однако, заметить, что аналитический расчет параметров и их погрешностей обычно не избавляет от необходимости строить графики, так как только с их помощью можно получить представление о полученной зависимости, отметить наличие существенных особенностей и т.д.
|

 (37)
(37)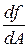 равна нулю, а вторая производная f" (А) =
равна нулю, а вторая производная f" (А) = 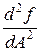 положительна, при этом значении А = А min. Для функции многих переменных эти условия заменяются требованием, чтобы частные производные, т. е. производные по параметру Ai, удовлетворяли вышеупомянутым условиям, причем все остальные параметры Aj (j
положительна, при этом значении А = А min. Для функции многих переменных эти условия заменяются требованием, чтобы частные производные, т. е. производные по параметру Ai, удовлетворяли вышеупомянутым условиям, причем все остальные параметры Aj (j  i) при вычислении производных считаются постоянными.
i) при вычислении производных считаются постоянными.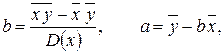 (38)
(38) (39)
(39) (40)
(40) (41)
(41)
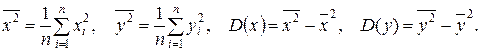 (42)
(42) зависимость давления насыщающих паров жидкости теоретически может быть представлена в виде
зависимость давления насыщающих паров жидкости теоретически может быть представлена в виде (43)
(43)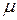 – молярная масса, R – универсальная газовая постоянная, T – абсолютная температура,
– молярная масса, R – универсальная газовая постоянная, T – абсолютная температура, 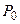 – некоторая постоянная.
– некоторая постоянная.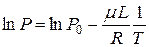 .
.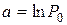 и
и  .
.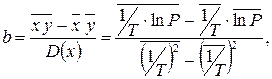
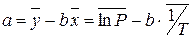 .
.


