Оценка случайной погрешности прямых измерений
Для оценки величины случайной погрешности отдельного измерения существует несколько способов. Наиболее распространена оценка с помощью среднеквадратичной погрешности,или стандартной погрешности
где Если измеряемая величина у является суммой (или разностью) двух величин х1 и х2, результаты измерений которых независимы, тогда погрешности суммируются по формуле:
Из закона сложения погрешностей (7) следует важный вывод, относящийся к определению погрешности результата серии измерений. Результат серии измерений отягчен меньшей ошибкой, чем результат каждого отдельного измерения. Средняя квадратичная погрешность
При практической работе важно строго разграничивать применение средней квадратичной ошибки одного измерения Последняя применяется всегда, когда нам нужно оценить погрешность того числа, которое мы получили в результате всех произведенных измерений. В тех случаях, когда мы хотим характеризовать точность применяемого способа измерений, следует характеризовать его ошибкой Если число измерений очень велико, то подверженная случайным колебаниям величина
Именно этот предел и называют генеральной средней квадратичной ошибкой (стандартной погрешностью) измерения. Квадрат этой величины называют дисперсией измерений. Соответственно
и
Относительная величина средней квадратичной погрешности, выраженная в процентах, носит название коэффициента вариации:
Назовем доверительным интервалом интервал
в который попадает истинное значение а измеряемой величины с заданной вероятностью. Надежностью результата серии измерений (или доверительной вероятностью) называется вероятность α того, что истинное значение а измеряемой величины попадает в данный доверительный интервал. Эта величина α выражаетсяили в долях единицы, или в процентах и показывает долю результатов (из общего числа измерений), погрешность которых не выходит за интервал ±Δ а. Чем больше величина доверительного интервала Для того чтобы получить оценки границ доверительного интервала для а при малых n (практически при n < 20) применяют коэффициент Стьюдента tα. Коэффициенты Стьюдента tα зависят от числа произведенных измерений n и от величины надежности α:
Задавая вероятность того, что истинное значение измеряемой величины а попадает в данный доверительный интервал, т. е., другими словами, задавая надежность α, равную определенной величине [3], по числу проведенных измерений п определяем значение коэффициента Стьюдента tα для этих данных[4]. Тогда, определив предварительно Δ a = tα · После этого результат измерений можно записать в виде
или
что означает, что истинное значение величины а попадает в доверительный интервал ( Таким образом, для характеристики величины случайной ошибки необходимо задать два числа: величину доверительного интервала и доверительную вероятность. Значение последней позволяет оценить степень надежности полученного результата[5]. Довольно часто доверительный интервал берут равным 3 Наряду со среднеквадратичной погрешностью иногда пользуются средней арифметической погрешностью, вычисляемой по формуле:
Точно так же, как и для средней квадратичной погрешности, истинное генеральное значение средней арифметической погрешности ρ определяется соотношением:
Относительная погрешность измерений определяется соотношением: ε; = При достаточно большом числе наблюдений (для n >30) между σ; и ρ; существуют простые соотношения [5]:
В большинстве случаев целесообразно пользоваться среднеквадратичной погрешностью, а не средней арифметической. В первую очередь потому, что, пользуясь стандартной погрешностью, легче определять доверительные вероятности, так как для этого существуют специальные таблицы. Преимуществом средней арифметической погрешности является то, что ее проще вычислять. Естественно, что при большом значении n безразлично, какой из погрешностей пользоваться, так как между ними существует вышеуказанное соотношение (19). При малом числе n всегда нужно пользоваться стандартной погрешностью или коэффициентом вариации.
|

 (6)
(6) – среднее арифметическое измеряемой величины, аi – результат отдельного измерения.
– среднее арифметическое измеряемой величины, аi – результат отдельного измерения. . (7)
. (7) результата серии измерений равна средней квадратичной погрешности отдельного результата, деленной на корень квадратный из числа измерений [3,4]
результата серии измерений равна средней квадратичной погрешности отдельного результата, деленной на корень квадратный из числа измерений [3,4] . (8)
. (8) и средней квадратичной ошибки результата серии измерений
и средней квадратичной ошибки результата серии измерений 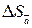 .
.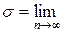
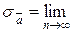
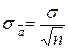 . (11)
. (11)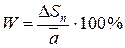 (12)
(12)
 . (13)
. (13) . (14)
. (14)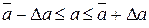
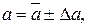 (α = …) (15)
(α = …) (15) ) с надежностью, равной α.
) с надежностью, равной α. , тогда вероятность того, что результаты измерений отличаются от истинного значения на величину, не большую Δ х (по таблице приложения 2), равна 0,997.
, тогда вероятность того, что результаты измерений отличаются от истинного значения на величину, не большую Δ х (по таблице приложения 2), равна 0,997. . (16)
. (16) . (17)
. (17)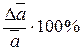 . (18)
. (18) = 1,25 или ρ = 0,85
= 1,25 или ρ = 0,85 


