Графическая обработка результатов измерений
Если изучается зависимость одной величины от другой, то результаты могут быть представлены в виде графика. При вычерчивании графика руководствуются следующими правилами[9]: Выбор бумаги. График строят только на миллиметровой бумаге или на бумаге со специальными координатными сетками. При их отсутствии иногда приходится (хотя это крайне нежелательно!) пользоваться бумагой «в клеточку» или белой бумагой, на которой карандашом нанесена сетка. Выбор координатных осей. Общепринято по оси абсцисс откладывать ту величину, изменения которой являются причиной изменения другой (т. е. по оси абсцисс – аргумент, по оси ординат – функцию). Выбор масштабов. Масштаб графика определяется погрешностью измерения величин, отложенных по осям: погрешность должна быть видна на графике, т. е. должна представляться в выбранном масштабе отрезком достаточной длины, иначе график не отражает всех деталей эксперимента и не может быть использован для графической обработки данных без потери точности. Шкала должна легко читаться, поэтому одна клетка масштабной сетки должна соответствовать удобному числу – 0,1; 0,2; 0,5; 1; 2; 5; 10;... (но не 2,5; 3; 4; 7; 1,13; и т.д.) единиц изображаемой на графике величины. При неудобном масштабе нанесение экспериментальных точек на график и использование графика требуют неоправданно большого времени и нередко сопровождаются досадными ошибками. Масштабы по обеим осям выбираются независимо друг от друга. Однако следует помнить, что график получается более наглядным, если основная часть кривой имеет наклон, не слишком отличающийся от 45°. В этом случае наиболее удобно анализировать форму кривой. Если при выборе масштабов для обеих осей на основе величин погрешностей график получается слишком растянутым в каком-либо направлении, то это означает, что измерения соответствующей величины проведены с излишне высокой точностью. При таких условиях разумно несколько увеличить масштаб по оси, для которой точность измерений меньше, а затем выбрать масштаб для второй оси так, чтобы график имел удобную форму, уже не обращая внимания на величину погрешности. Нанесение шкал по осям. Оси графика должны иметь ясные, четкие обозначения. Рядом с делениями – на удобных расстояниях – должны быть нанесены цифры, позволяющие установить значения, соответствующие делениям шкалы. Масштаб наносится на осях графика в виде равноотстоящих «круглых» чисел, например 6; 8; 10;... или 4,74; 4,76; 4,78;... (чтобы не загромождать график, можно опускать целую часть числа: 4,74;,76;,78; и т.д.). Не следует расставлять эти числа слишком густо – достаточно нанести их через 2 или даже через 5 см. Это не вызывает неудобств, так как при рассмотрении графика можно легко восстановить пропущенные значения. Круглые значения цифр располагаются на жирных линиях сетки (на миллиметровой бумаге такие линии идут через 5 см). На оси обязательно указываются обозначение и единицы измерения соответствующей величины. При этом множитель, определяющий порядок величины, включается обычно в единицы измерения, например: I, мА; I, 103 А или, иногда, I· 103, А. Выбор интервала. При построении графиков следует разумно выбирать интервал, чтобы измеренные точки располагались на всей площади листа. Поэтому на графике приводится только та область изменения измеренных величин, которая была исследована на опыте. Не следует стремиться к тому, чтобы на графике обязательно поместилось начало координат (точка 0,0). Даже в том случае, когда требуется найти точку пересечения какой-либо прямой на графике с одной из координатных осей, нет необходимости, чтобы эта ось помещалась на графике; точку пересечения легко найти расчетом, пользуясь подобием треугольников. Начало координат помещают на графике только в том случае, когда это не требует большого увеличения его размеров. Следует помнить, однако, что иногда точка (0,0) есть результат измерения, причем часто – наиболее надежный результат (например, при определении сопротивления точка I = 0; U= 0). Нанесение точек на график. Точки должны наноситься на график очень тщательно и аккуратно, чтобы график получился более точным. Их следует отмечать карандашом, так как иначе ошибочно нанесенную точку нельзя удалить с графика, не испортив его. Никаких выносных линий и отметок, поясняющих построение точек,награфик наносить нельзя (так как они загромождают рисунок и мешают анализировать результаты). Выносная линия может в виде исключения быть нанесена, только если какую-либо точку хотят особо выделить на графике (например, положение максимума). Если на один и тот же график наносятся различные группы данных (результаты измерения разных величин; одной величины, но полученные в разных условиях или разными авторами и т. п.), то точки, относящиеся к разным группам, должны быть помечены различными символами (кружки, треугольники, звездочки и т. п.) или нанесены разными цветами, чтобы их нельзя было спутать. Изображение погрешности. Способ изображения на графике экспериментальных результатов зависит от того, известна ли их случайная погрешность. Если она неизвестна (что чаще всего и бывает), то результаты изображаются точками, а если известна, то лучше изображать их с помощью крестиков соответствующих размеров, нанесенных поверх точек. Полуразмер креста по горизонтали должен быть равен стандартной погрешности по оси абсцисс, а его вертикальный полуразмер – погрешности по оси ординат. В том случае, если одна из ошибок – из-за своей малости – не может быть изображена графически, результаты изображаются черточками, вытянутыми на ± σ; в том направлении, где погрешность не мала. Можно также указывать погрешность размером точек, для этого точки рисуют либо в виде эллипсов с длиной полуосей, равной в масштабе графика величине погрешности, либо в виде прямоугольников таких же размеров. Нет необходимости указывать погрешность для каждой точки, но если погрешность изменяется вдоль кривой, следует показать это на нескольких точках. Проведение кривых через экспериментальные точки. Кривую на графике проводят плавно, избегая изломов и перегибов. Кривая должна проходить насколько возможно ближе ко всем нанесенным точкам, но ни в коем случае не следует стремиться провести ее через каждую точку. Через экспериментальные точки всегда следует проводить самую простую кривую, совместимую с этими точками, т. е. кривую, от которой экспериментальные данные отступают, как правило (в 2/3 случаев), не более чем на стандартную ошибку. Не следует придавать кривым никаких изгибов, если экспериментальным данным – в пределах ошибок – можно удовлетворить и без этого. Излом на кривой можно рисовать только в том случае, если он не может быть объяснен погрешностью измерений и если при этом на его существование указывает большое число точек. Кроме того, нужно быть уверенным в отсутствии систематических ошибок (изломы часто появляются, например, когда сначала работают на одной шкале прибора, а затем переходят на другую). Помните, что всякая особенность на кривой (излом, резкое изменение кривизны и пр.) требует либо специального экспериментального доказательства, либо теоретического объяснения. При проведении кривой нужно следить за тем, чтобы на каждом достаточно большом ее участке экспериментальные точки располагались как выше, так и ниже кривой. Во всех случаях кривая должна быть проведена так, чтобы она не закрывала экспериментальных точек. Выбор наиболее наглядной зависимости. При построении графика нужно стремиться к тому, чтобы он наиболее четко отражал все особенности представляемой зависимости. Для этого часто бывают удобны функциональные масштабы – по осям откладываются не сами измеряемые величины, а их функции, подобранные в соответствии с решаемой задачей. При графической обработке результатов следует помнить, что на глаз можно точно провести через экспериментальные точки только прямую линию. Поэтому при построении графика следует стремиться к тому, чтобы ожидаемая зависимость имела вид прямой линии. К логарифмическому масштабу без особой необходимости прибегать не следует. Одна из наиболее часто встречающихся погрешностей опыта – смещение нуля отсчета – приводит в этом случае к сильному искажению прямолинейного характера кривой. Бывают, однако, случаи, когда логарифмический масштаб необходим. Это происходит, например, если исследуемая величина очень сильно изменяется, причем одновременно интересны очень малые и очень большие ее значения. Логарифмический масштаб позволяет все точки уместить на одном чертеже и исследовать совместно. Логарифмический масштаб выбирают и в том случае, если имеются основания ожидать, что искомая зависимость является степенной, но показатель степени неизвестен. Иногда применяют также полулогарифмический (логарифм откладывается только по одной из осей) масштаб. Надо помнить, однако,что логарифмический масштаб можно применять без потери точности, только если относительная погрешность постоянна для всей кривой. Оформление графиков. Готовый график снабжается заголовком, который должен содержать точное описание того, что показывает график. Разные группы точек (разные символы) или разные кривые на графике также должны быть объяснены. Эти объяснения приводятся в подписи к графику (внизу листа или на свободном, не занятом кривой, месте на самом графике).
Основное достоинство графиков – их наглядность. Посмотрев на график, можно получить качественное представление о полученной зависимости и отметить наличие различных особенностей: максимумов, минимумов, точек перегиба, областей наибольшей и наименьшей скорости изменения, периодичности и т. п. График позволяет также легко судить о соответствии экспериментальных данных той или иной теоретической зависимости и вообще облегчает обработку измерений. С помощью графика можно вести обработку экспериментальных данных. Графическая обработка не так точна, как численная, использующая строгие методы, например метод наименьших квадратов (см. ниже), но зато проста, наглядна и в большинстве случаев не требует длинных вычислений, давая в то же время очень неплохие результаты. Более того, на графике обычно хорошо видны особенности, которые легко пропустить при формальном применении численных методов. Поэтому первичную обработку данных (особенно, если она проводится непосредственно во время эксперимента) желательно делать графически. Конечно, если полученной точности окажется недостаточно, то нужно использовать более точные методы. Очень часто бывает нужно выразить найденную из опыта зависимость в виде уравнения (например, представить ее в виде полинома у = a+bx+cx2+..., показательной функции у = аеbx и т. п.). Вид этого уравнения может быть подобран произвольно или получен на основании каких-либо теоретических соображений. В обоих случаях необходимо проверить, пригодна ли данная формула для представления совокупности экспериментальных данных, и подобрать наилучшим образом значения неизвестных параметров а, b, с,..., входящих в формулу. Особенно просто задача решается для линейной функции у = а + bх. (32) (т. е. для простых формул, содержащих один или два неизвестных параметра). В этом случае график у (х) – прямая линия и необходимо найти параметры а и b в формуле (32). Значение b находится как угловой коэффициент полученной прямой [10], а значение а – как величина отрезка, отсекаемого ею на оси ординат [6]. Чтобы найти погрешность в определении параметра а, нужно смещать прямую вниз параллельно самой себе, пока выше нее не окажется вдвое больше точек, чем снизу. Затем следует сместить ее вверх, пока снизу не окажется вдвое больше точек, чем сверху. Пусть расстояние между этими прямыми ровно Δ а (см. рис. 1).
Рис. 1. Графический метод обработки результатов. Оценка погрешности в определении параметра a [6].
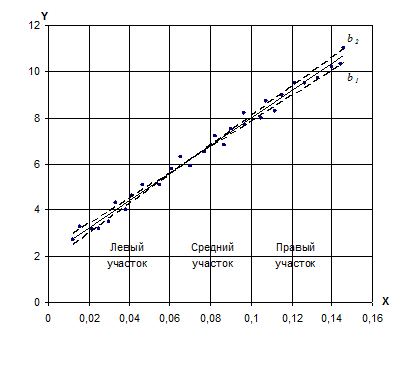
Рис. 2. Графический метод обработки результатов. Оценка погрешности в определении параметра b [6].
Погрешность в определении а равна [6]
где п — полное число точек на графике. Погрешность в определении параметра b находится аналогичным образом (рис. 2). «Рабочий участок» оси абсцисс (участок, на котором расположены экспериментальные точки) делится на три равные части. Средний участок в дальнейшей работе не участвует. Для определения
где п — полное число точек на графике. Часто случается, что начальная точка искомой зависимости хорошо известна и лежит в начале координат. Как бы ни была сложна зависимость тока, проходящего через проводник, от приложенного к нему напряжения, можно быть уверенным, что при отсутствии напряжения нет и тока (мы предполагаем, что в цепи не возникает термо-э.д.с.). Если чайник не нагревать и не охлаждать, то изменение его температуры равно нулю, и т. д. Во всех этих случаях нулевая точка не просто известна,— она является самой надежной из всех, которые используются при обработке результатов. Задача о проведении наилучшей прямой сводится в этом случае к подбору параметра в формуле у = k x. (35) Стандартная погрешность при определении параметра
где п — полное число точек на графике. Если функция у = f (x) нелинейна, удобно использовать функциональный масштаб – график перечерчивается в новых координатах, выбранных так, чтобы получить линейную зависимость. Зависимость вида у = a xn, например, можно исследовать на графике Если применяется такой метод обработки результатов, то, как правило, строят два графика – график в функциональном масштабе для количественной обработки и график в натуральном масштабе для наглядного представления функции.
|



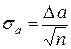 , (33)
, (33)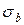 прямая поворачивается так, чтобы на левом участке выше нее оказалось вдвое больше точек, чем под ней, а на правом участке – наоборот. Затем кривая поворачивается так, чтобы на левом участке 2/3 точек лежали ниже прямой, а на правом – ниже нее. Обозначим разницу в угловых коэффициентах этих прямых через Δ b. Тогда
прямая поворачивается так, чтобы на левом участке выше нее оказалось вдвое больше точек, чем под ней, а на правом участке – наоборот. Затем кривая поворачивается так, чтобы на левом участке 2/3 точек лежали ниже прямой, а на правом – ниже нее. Обозначим разницу в угловых коэффициентах этих прямых через Δ b. Тогда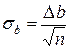 , (34)
, (34)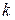 в формуле (35) находится следующим образом. «Рабочим» участком в этом случае является весь диапазон по оси Х от нуля до последней точки. Его следует разбить на три части и самую левую – ближнюю к началу координат – часть во внимание не принимать. Затем нужно провести через начало координат две вспомогательные прямые так, чтобы выше одной из них лежало 2/3 точек, а выше другой – 1/3. Различие в
в формуле (35) находится следующим образом. «Рабочим» участком в этом случае является весь диапазон по оси Х от нуля до последней точки. Его следует разбить на три части и самую левую – ближнюю к началу координат – часть во внимание не принимать. Затем нужно провести через начало координат две вспомогательные прямые так, чтобы выше одной из них лежало 2/3 точек, а выше другой – 1/3. Различие в 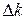 . Стандартная погрешность находится по формуле
. Стандартная погрешность находится по формуле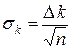 , (36)
, (36)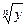 = f (x) или у = f (xn), если п известно. Если же п, как и а, подлежит определению из экспериментальных данных, применяется логарифмический масштаб lg y = f (lg x), в котором подбираемая функция представится прямой lg y = lg a + n lg x; параметры функции легко определяются из наклона и начальной ординаты прямой. Функция вида у = а + b х2 подбирается на графике у = f (x2). Экспоненциальная функция вида y = a x2 e-bx (температурная зависимость тока термоэлектронной эмиссии) изобразится прямой в координатах lg y/x2 и 1/х.
= f (x) или у = f (xn), если п известно. Если же п, как и а, подлежит определению из экспериментальных данных, применяется логарифмический масштаб lg y = f (lg x), в котором подбираемая функция представится прямой lg y = lg a + n lg x; параметры функции легко определяются из наклона и начальной ординаты прямой. Функция вида у = а + b х2 подбирается на графике у = f (x2). Экспоненциальная функция вида y = a x2 e-bx (температурная зависимость тока термоэлектронной эмиссии) изобразится прямой в координатах lg y/x2 и 1/х.


