Общая погрешность прямых измерений. Выбор необходимого числа измерений
Как было показано выше, погрешность прямых измерений складывается из систематических и случайных погрешностей. Увеличивая число измерений, мы можем сделать случайную ошибку как угодно малой. Но точность измерения не может быть больше той, которую позволяет измерительный прибор. Таким образом, инструментальная погрешность - это минимальная погрешность, которую можно получить в процессе измерения данным прибором. Точность однократного измерения определяется точностью измерительного прибора. Сколько нужно произвести измерений для достижения наибольшей точности? Всегда ли нужно производить измерения многократно? Решая вопрос о количестве измерений всегда нужно помнить, что многократные измерения необходимы не для вычисления погрешностей, а для увеличения точности конечного результата. Уменьшения случайной погрешности результата можно добиваться двумя путями: 1) совершенствовать технику измерений для улучшения точности, т. е. для уменьшения σ;, и 2) увеличивать число измерений, т. е. использовать соотношение Однако при наличии систематической погрешности, которая связана с погрешностью измерительного прибора, повторные измерения не приведут к повышению точности. Выполненные тем же самым прибором, они не позволяют ни обнаружить, ни устранить систематическую ошибку. Уменьшать случайную погрешность целесообразно до тех пор, пока общая погрешность измерений не будет полностью определяться систематической ошибкой. Для этого нужно, чтобы доверительный интервал был бы существенно меньше величины систематической ошибки. Достаточно, чтобы он был меньше хотя бы в 3 или даже в 2 раза. Таким образом, при выборе числа необходимых измерений, будем руководствоваться следующими правилами: 1. Если случайная погрешность является определяющей, то измерение следует производить несколько раз. Число измерений целесообразно выбрать таким, чтобы случайная погрешность была меньше систематической хотя бы в 2 - 3 раза. Тогда последняя будет определять окончательную погрешность результата. 2. Если систематическая погрешность является определяющей, т. е. ее величина существенно больше случайной погрешности, присущей данному методу, то достаточно выполнить измерения один раз. Этот случай имеет место, если при многократных измерениях повторяется один и тот же результат или если повторные измерения просто невозможны. В таких случаях погрешность результата задается погрешностью измерительного прибора. Результат единичного измерения величины х может быть записан в виде х = х' ± Δ хинстр, где х ' - результат единственного измерения. З. Если систематическая и случайная погрешности измерений близки друг к другу и обе в одинаковой степени определяют точность результата, тогда полная погрешность определяется квадратным корнем из суммы квадратов систематической и случайной ошибок:
или
для среднеквадратичной (стандартной) погрешности. Этот случай будет иметь место тогда, когда нереально произвести столько измерений, чтобы сделать Δ хсл<<;Δ хсист, а также при выполнении студентами учебной лабораторной работы, когда выполняют только лишь запланированное число измерений. Формула (20) показывает, что при наличии как случайной, так и систематической погрешности полная ошибка опыта больше, чем каждая из них в отдельности. Из этого равенства следует, что ошибка прямых измерений никогда не может быть меньше инструментальной погрешности: Δ х ≥; Δ хсист, а с увеличением числа измерений (при n→∞;) Δ х →; Δ хсист. Если же отклонение результатов отдельных измерений от среднего значения существенно превосходят значение систематической погрешности Δ хсл>>;Δ хсист, и нет возможности увеличить число измерений, например, при выполнении лабораторной работы, то можно пренебречь систематической погрешностью измерений и считать, что полная погрешность примерно равна случайной погрешности Δ х ≈; Δ хсл.
|

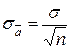 .
.
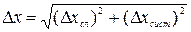 (20)
(20)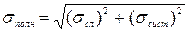 (21)
(21)


