Измерения, показатели точности измерений
Часть первая Оценка погрешностей измерений. Запись и обработка результатов [1]
В точных науках, в частности в физике, особое значение придают проблеме оценки точности измерений. Что никакое измерение не может быть абсолютно точным – факт общефилософского значения. Т.е. в процессе проведения эксперимента мы всегда получаем приближенное значение физической величины, лишь приближаясь в той или иной степени к ее истинному значению. Измерения, показатели точности измерений Физика, как одна из естественных наук, изучает окружающий нас материальный мир, пользуясь физическим методом исследования, важнейшей составляющей которого является сравнение полученных теоретическим расчетом данных с экспериментальными (измеренными) данными. Важнейшей частью процесса обучения физике в университете является выполнение лабораторных работ. В процессе их выполнения студенты проводят измерения различных физических величин. При измерении физические величины выражаются в виде чисел, которые указывают, во сколько раз измеренная величина больше или меньше другой величины, значение которой принято за единицу. Т.е. под измерением понимается «познавательный процесс, заключающийся в сравнении путем физического эксперимента данной физической величины с известной физической величиной, принятой за единицу измерения» [2]. Измерения выполняются с помощью мер и измерительных приборов. Мерой называют вещественное воспроизведение единицы измерений, долевого или кратного ее значения (гиря, измерительная колба, магазины электрических сопротивлений, емкостей и т.п.). Измерительным прибором называют средство измерения, дающее возможность непосредственно отсчитывать значение измеряемой величины. Вне зависимости от назначения и принципа действия любой измерительный прибор можно характеризовать четырьмя параметрами: 1) Пределы измерения указывают диапазон измеряемой величины, доступный данному прибору. Например, штангенциркуль измеряет линейные размеры в пределах от 0 до 18 см, а миллиамперметр - токи от -50 до +50 mA и т.д. На некоторых приборах можно изменять (переключать) пределы измерения. Многопредельные приборы могут иметь несколько шкал с разным числом делений. Отсчет следует проводить по той шкале, у которой число делений кратно верхнему пределу прибора. 2) Цена деления C определяет,сколько единиц измерения (или их долей) содержится в одном (наименьшем) делении шкалы прибора. Например, цена деления микрометра C = 0,01 мм/деление (или 10 мкм/дел), а для вольтметра C = 2 В/дел и т.д. Если по всей шкале С одинакова (равномерная шкала), то для определения цены деления нужно предел измерения прибора хном разделить на число делений шкалы прибора N:
3) Чувствительность прибора α показывает, сколько минимальных делений шкалы приходится на единицу измеряемой величины или какую-либо ее долю. Из этого определения следует, что чувствительность прибора – это величина, обратная цене деления: α = 1/С. Например, чувствительность микрометра можно оценить величиной α = 1/0,01 = 100 делений/мм (или α = 0,1 дел/мкм), а для вольтметра α = 1/2 = 0,5 дел/В и т. д. 4) Точность прибора характеризует величину абсолютной погрешности, которая получается в процессе измерения этим прибором. Характеристикой точности измерительных приборов служит предельная погрешность градуировки Δ xград. На шкале или в паспорте прибора приводится максимальная абсолютная или относительная погрешность градуировки либо указывается класс точности, который определяет систематическую погрешность прибора. В порядке возрастания точности электроизмерительные приборы делятся на восемь классов: 4,0; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1 и 0,05. Число, обозначающее класс точности, наносится на шкалу прибора[2] и показывает наибольшее допустимое значение основной погрешности в процентах от предела измерения хном Кл. точности = εпр= Есть приборы (преимущественно высокой точности), класс точности которых определяет относительную погрешность прибора по отношению к измеренной величине. Если на приборах и в их паспортах нет данных о классе точности и не указана формула расчета погрешности, то инструментальную погрешность следует считать равной половине цены деления прибора. Измерения разделяют на прямые и косвенные. При прямых измерениях искомую физическую величину устанавливают непосредственно из опыта. Значение измеряемой величины отсчитывается при этом по шкале прибора или подсчитывается число и значение мер, разновесок и т. д. Прямыми измерениями являются, например, взвешивание на весах, определение линейных размеров тела правильной формы с помощью штангенциркуля, определение времени по секундомеру и т. д. При косвенных измерениях измеряемая величина определяется (вычисляется) из результатов прямых измерений других величин, которые связаны с измеряемой величиной определенной функциональной зависимостью. Примеры косвенных измерений – определение площади стола по его длине и ширине, плотности тела по измерениям массы и объема тела и т. п. Качество измерений определяется их точностью. При прямых измерениях точность опытов устанавливается из анализа точности метода и приборов, а также из повторяемости результатов измерений. Точность косвенных измерений зависит как от надежности используемых для расчета данных, так и от структуры формул, связывающих эти данные с искомой величиной. Точность измерений характеризуется их погрешностью. Абсолютной погрешностью измерений
Для оценки точности любых измерений вводят также понятие относительной погрешности. Относительная погрешность измерения – это отношение абсолютной погрешности измерения к истинному значению измеряемой величины (может быть выражена в процентах).
Как следует из (3) и (4), для того, чтобы найти абсолютную и относительную погрешность измерений, нужно знать не только измеренное, но и истинное значение интересующей нас величины. Но если истинное значение известно, то незачем производить измерения. Цель измерений всегда состоит в том, чтобы узнать неизвестное заранее значение физической величины и найти, если не ее истинное значение, то хотя бы значение, достаточно мало от него отличающееся. Поэтому формулы (3) и (4), определяющие величину погрешностей, для практики непригодны. Часто вместо хист используют среднее арифметическое значение по нескольким измерениям
где хi – результат отдельного измерения.
|

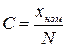 . (1)
. (1) . (2)
. (2)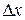 называют разность между найденным на опыте хизм и истинным значением физической величины хист
называют разность между найденным на опыте хизм и истинным значением физической величины хист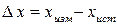 . (3)
. (3) . (4)
. (4) , (5)
, (5)


