Задачи и решения.
2.4.1. Критерий устойчивости Гурвица. Для систем первого и второго порядков необходимым и достаточным условием устойчивости является положительность (или отрицательность) всех коэффициентов характеристического уравнения. Задача А1. Дана система автоматического регулирования, структурная схема которой имеет следующий вид:
Можно ли подобрать такое значение коэффициента К, чтобы замкнутая система была устойчива? Решение: определяем передаточную функцию замкнутой системы
ее характеристическое уравнение Поскольку коэффициент при р равен нулю, невозможно выполнить достаточное условие устойчивости системы третьего порядка. Поэтому система будет неустойчивой при любых значениях К.
Задача N2. Дана система
Определить предельное значение коэффициента К, при котором замкнутая система находится на границе устойчивости, если переходная характеристика h(t) звена с передаточной функцией W1(p) описывается выражением
Решение: Отыскиваем изображение переходной характеристики и определяем передаточную функцию звена W1(p).
Определяем передаточную функцию замкнутой системы и ее характеристическое уравнение:
Условие нахождения системы на границе устойчивости определяем с помощью критерия Гурвица:
Задача N3. Дана система
Оценить с помощью критерия Гурвица устойчивость системы. Решение: Для системы четвертого порядка необходимым и достаточным условием устойчивости является:
Находим передаточную функцию замкнутой системы и ее характеристическое уравнение
Подставив заданные значения коэффициентов и параметров системы в необходимое условие устойчивости, получим:
Задача N4. Дана система, структурная схема которой имеет следующий вид:
При каких значениях коэффициента обратной связи К1 система в замкнутом состоянии устойчива. Решение: Определим передаточную функцию замкнутой системы
Ее характеристическое уравнение:
Задача N 5. Дана структурная схема системы:
Определить, при каких значениях коэффициента К замкнутая система устойчива, если импульсная переходная характеристика звена с передаточной функцией Решение: находим изображение импульсной переходной характеристики, которое совпадает с передаточной функцией звена
Определяем передаточную функцию замкнутой системы:
Ее характеристическое уравнение
Задача N6. Дана система:
При каких значениях постоянной времени Решение: Находим характеристическое уравнение замкнутой системы
Условие устойчивости системы третьего порядка:
Разделим обе части неравенства на
Раскроем скобки и перенесем единицу влево:
Умножим обе части на
Подставим в полученное выражение заданные значения параметров:
или
Задача N7. Дана система
Оценить устойчивость системы, если Решение: С помощью правил структурных преобразований преобразуем исходную схему в типовую одноконтурную с обратной связью, для этого перенесем узел со входа звена с передаточной функцией равной
Определим передаточные функции внутренних контуров с обратной связью
Определим передаточную функцию замкнутой системы и ее характеристическое уравнение
С учетом заданных параметров системы характеристическое уравнение примет следующий вид:
Согласно критерию Гурвица, поскольку
Критерий устойчивости Рауса.
Задача N8. Дано характеристическое уравнение замкнутой системы:
Все коэффициенты
Определим знак коэффициентов первого столбца матрицы:
Поскольку коэффициенты
Критерий устойчивости Михайлова.
Задача N9. Передаточная функция разомкнутой системы имеет вид:
С помощью критерия Михайлова определить предельное значение общего коэффициента передачи разомкнутой системы К, при котором система окажется на границе устойчивости. Решение: Характеристический полином замкнутой системы имеет вид:
При нахождении системы на границе устойчивости кривая Михайлова проходит через начало координат при некотором значении частоты
Из последнего выражения находим значение квадрата частоты, при которой кривая Михайлова проходит через начало координат
Задача N 10. Дано характеристическое уравнение замкнутой системы:
Оценить устойчивость системы с помощью критерия Михайлова. Решение: Подставив в исходное выражение
Подставив исходные данные, получим следующие уравнения:
Находим корни уравнений
Построение областей устойчивости.
Задача N 11. Дана система.
Решение: Характеристический полином имеет вид:
Поскольку для устойчивости системы необходимо, чтобы все коэффициенты характеристического уравнения были положительны,
Из последнего равенства имеем:
С учетом заданных значений параметров системы Область устойчивости в плоскости параметров
|





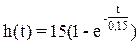
 ;
; 

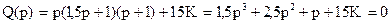
 ; Кпр=0,11.
; Кпр=0,11.

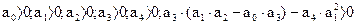 .
. 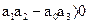

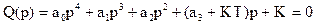
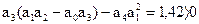 . Таким образом, система устойчива.
. Таким образом, система устойчива.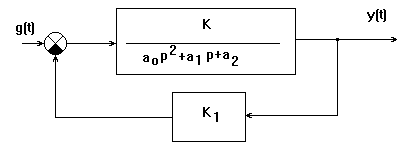
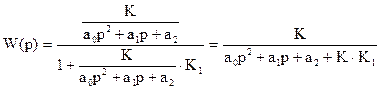
 , необходимое и достаточное условие устойчивости системы второго порядка состоит в положительности всех коэффициентов характеристического уравнения:
, необходимое и достаточное условие устойчивости системы второго порядка состоит в положительности всех коэффициентов характеристического уравнения: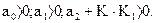 Отсюда следует, что
Отсюда следует, что  , то есть система устойчива при любом положительном К1.
, то есть система устойчива при любом положительном К1.
 описывается выражением
описывается выражением 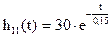 .
. .
.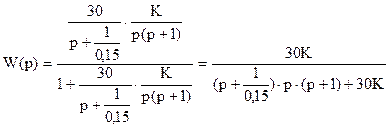
 , для устойчивости системы необходимо и достаточно чтобы
, для устойчивости системы необходимо и достаточно чтобы  . Подставив в последнее выражение заданные значения параметров определяем значения К, при которых система устойчива.
. Подставив в последнее выражение заданные значения параметров определяем значения К, при которых система устойчива. 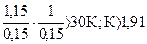 .
.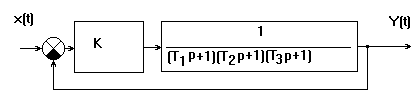
 система устойчива, если
система устойчива, если 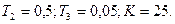



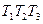 , при этом получим
, при этом получим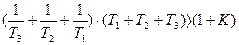
 или
или 
 , перенеся
, перенеся 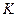 влево:
влево: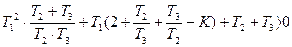
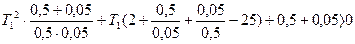
 . Функция
. Функция  представляет собой уравнение параболы. Функция
представляет собой уравнение параболы. Функция  при
при 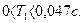 и
и 

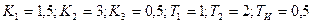
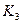 на его выход. При этом структурная схема примет следующий вид:
на его выход. При этом структурная схема примет следующий вид:


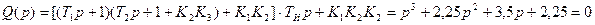
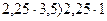 рассматриваемая система устойчива.
рассматриваемая система устойчива.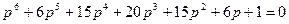
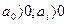 . Составим матрицу Рауса, первый столбец которой содержит 7 коэффициентов:
. Составим матрицу Рауса, первый столбец которой содержит 7 коэффициентов:

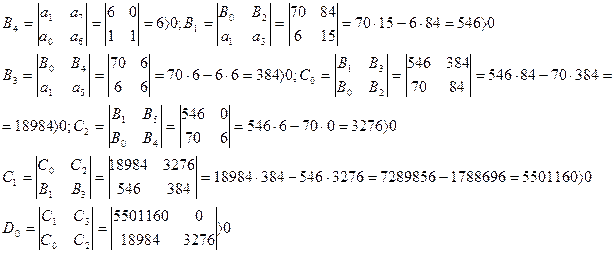
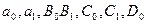 положительны, рассматриваемая система шестого порядка устойчива.
положительны, рассматриваемая система шестого порядка устойчива. , где К – общий коэффициент передачи разомкнутой системы.
, где К – общий коэффициент передачи разомкнутой системы.  - постоянные времени.
- постоянные времени.
 . После подстановки численных значений постоянных времени и
. После подстановки численных значений постоянных времени и  получим:
получим: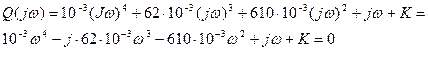
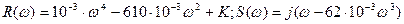
 . Поэтому при
. Поэтому при 

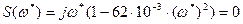
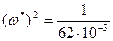 . Подставив полученное значение частоты в уравнение
. Подставив полученное значение частоты в уравнение 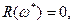 после преобразований получим
после преобразований получим 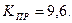
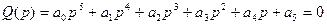 ,
, 
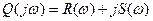 , где
, где  ;
; 

 и
и 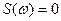
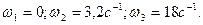 Поскольку корни уравнений
Поскольку корни уравнений  перемежаются, кривая Михайлова последовательно проходит пять квадрантов, нигде не превращаясь в нуль. Следовательно, система устойчива.
перемежаются, кривая Михайлова последовательно проходит пять квадрантов, нигде не превращаясь в нуль. Следовательно, система устойчива.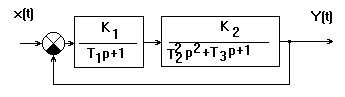
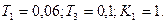 Построить область устойчивости на плоскости параметров системы
Построить область устойчивости на плоскости параметров системы 
 , после преобразований получим:
, после преобразований получим:
 . Отсюда следует, что
. Отсюда следует, что  . Необходимое и достаточное условие устойчивости системы определяется следующим равенством:
. Необходимое и достаточное условие устойчивости системы определяется следующим равенством: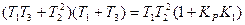 .
. или
или 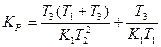
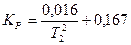
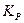 и
и  имеет следующий вид:
имеет следующий вид:



