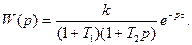Математические модели цифровых систем управления.
3.2.1. Основные положения. Математические модели цифровых систем управления классифицируются в зависимости от вида аргумента. Различают следующие виды математических моделей: 1) временные – аргумент дискретное время - разностные уравнения; - переходная характеристика; - функция веса. 2) операторные – аргумент либо оператор z, либо оператор w - передаточные функции. 3) частотные – аргумент частота - частотные характеристики. 3.2.2. Разностные уравнения связи n-порядка между входом и выходом. Если в непрерывных системах управления основной временной математической моделью является дифференциальное уравнение, основными элементами которого являются производные различных порядков, то в цифровых системах управления основной временной математической моделью является разностное уравнение n-го порядка, элементами которого являются разности различных порядков. Вид разностного уравнения зависит от способа представления разностей. Различают два способа представления разностей, как эквивалентов производных непрерывной функции: - прямые (правые) разности; - обратные (левые) разности. В прямых разностях используется строгое понятие производной непрерывной функции, поэтому прямая разность, например первого порядка, в момент Обратная разность, например, первого порядка, определяется по предшествующему значению решетчатой функции в момент времени Разность более высокого порядка может быть представлена не только через разности более низкого порядка, но и через значения функции в различные моменты времени. Таким образом, разностные уравнения n-го порядка в общем случае при одном входном воздействии имеют следующий вид: - для прямых разностей
- для обратных разностей
В приведенных уравнениях для сокращения записи опущено 3.2.3 Система разностных уравнений первого порядка (система уравнений параметров состояния). Исходным для получения системы разностных уравнений первого порядка, т.е. уравнений параметров состояния цифровой системы управления, может служить разностное уравнение n-го порядка. Как следует из п.3.2.2 для прямых разностей разностное уравнение n-го порядка имеет вид:
Система разностных уравнений первого порядка получается путем введения следующих переменных, параметров состояния, и имеет следующий вид
В частном случае при
Систему уравнений для параметров состояния обычно представляют в векторно-матричной форме:
В общем виде в удобной форме записи система уравнений параметров состояния имеет вид:
Матрицы Для обратных разностей разностное уравнение имеет вид:n-го порядка
В этом случае система разностных уравнений первого порядка получается путем введения следующих переменных, параметров состояния, и имеет следующий вид:
В частном случае при
Систему уравнений для параметров состояния в этом случае также представляют в векторно-матричной форме:
Так же, как и для прямых разностей, для обратных разностей в удобной форме система уравнений параметров состояния имеет вид:
3.2.4.Основные понятия о передаточных функциях цифровых систем управления. Общие положения. Передаточные функции являются функциями определенного оператора. В непрерывных системах управления таким оператором является оператор Р. Для анализа и синтеза цифровых систем управления могут применяться две разновидности передаточных функций: - передаточная функция - передаточная функция Связь между операторами передаточных функций устанавливается следующими соотношениями:
Передаточная функция Передаточная функция 1) исходным является разностное уравнение связи между входом и выходом; 2) исходной является передаточная функция в непрерывной форме. В первом случае необходимо найти
Во втором случае для получения передаточной функции Таблица изображений по Лапласу и
Большинство передаточных функций непрерывной части системы управления содержит запаздывающее звено, а именно
где
В этом случае для получения цифрового эквивалента непрерывной части удобно воспользоваться соотношением операторов
где Тогда в соответствии с соотношением для операторов получаем:
После этого необходимо воспользоваться приведенным выше правилом для преобразования
3.2.5. Передаточные функции устройств связи с объектом управления. В ряде случаев невозможно непосредственно отнести устройство связи с объектом управления ни к цифровой, ни к непрерывной части системы. Примером таких устройств является фиксирующее звено нулевого порядка, передаточная функция которого содержит оператор
В этом случае составляющая
Передаточная функция Для получения передаточной функции
3. 2.6. Передаточные функции цифровых систем управления. Обобщенная структурная схема системы. Используя структурные преобразования можно цифровую систему управления любой сложности привести к некоторой обобщенной структурной схеме:
В частном случае
В частном случае Передаточные функции цифровых систем управления. 1) передаточная функция разомкнутой системы
2) передаточные функции замкнутой системы Вид передаточной функции замкнутой системы зависит от того, что принимается за “выход” и “вход” системы.
3.2.7. Частотные характеристики. Частотные характеристики получаются при помощи перехода от операторного описания цифровой системы управления к частотному путем соответствующей замены в передаточной функции оператора. При этом операторы заменяются следующим образом:
где
При переходе в частотную область путем непосредственной замены в передаточной функции оператора z, частотные характеристики цифровых систем управления имеют периодический характер с периодом
3.2.8. Задачи. А. Задано: разностное уравнение разомкнутой системы управления А1. A3. А5. А7. А9. А11. А13. А15. А17. А19. Определить: - передаточную функцию разомкнутой системы - разностное уравнение замкнутой системы; - уравнение параметров состояния замкнутой системы; - непрерывный эквивалент разомкнутой цифровой системы управления - частотные характеристики разомкнутой системы в функции псевдочастоты
Б. Задано: передаточная функция непрерывной части системы управления. Б1. Б3.
Определить: передаточную функцию В. Задано: Передаточная функция непрерывной части системы управления. Устройство связи с объектом управления – фиксирующее звено нулевого порядка. В1. В5. В8. Определить эквивалентную передаточную функцию в цифровой форме
|


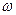 , либо псевдочастота
, либо псевдочастота 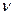
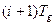 . Решетчатая функция
. Решетчатая функция 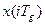 - это функция, значения которой определены только в дискретные моменты времени.
- это функция, значения которой определены только в дискретные моменты времени.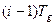 .
.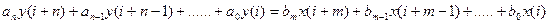
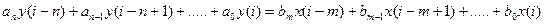
 , то есть по существу принято
, то есть по существу принято 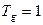 с. Наибольший порядок разности соответствует наибольшему сдвигу вправо или влево относительно рассматриваемого момента времени
с. Наибольший порядок разности соответствует наибольшему сдвигу вправо или влево относительно рассматриваемого момента времени 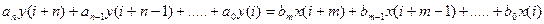





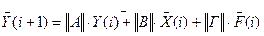
 ,
, 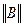 и
и 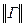 имеют определенный смысл, а именно, матрица
имеют определенный смысл, а именно, матрица 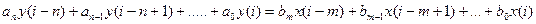
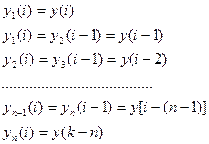
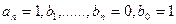



 , аргументом которой является оператор z. Эта передаточная функция непосредственно представляет цифровую систему управления;
, аргументом которой является оператор z. Эта передаточная функция непосредственно представляет цифровую систему управления; , аргументом которой является оператор
, аргументом которой является оператор 
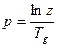


 изображения выходной величины к
изображения выходной величины к 
 необходимо передаточную функцию
необходимо передаточную функцию 
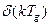

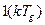

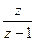
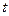

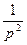
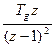


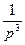



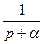
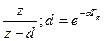
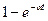
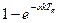

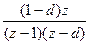
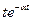
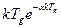
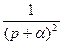
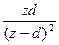
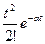




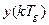
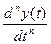
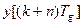
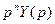
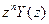
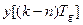



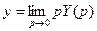
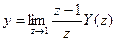
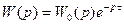 ,
,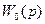 - не содержит элементов запаздывания;
- не содержит элементов запаздывания; - время запаздывания.
- время запаздывания.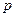 и
и  , предварительно выразив запаздывание
, предварительно выразив запаздывание 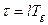
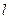 - целое число.
- целое число.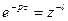
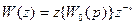 .
.
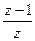 переносится в дискретную часть системы, а составляющая
переносится в дискретную часть системы, а составляющая 
 .
.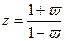 . После преобразования передаточной функции
. После преобразования передаточной функции 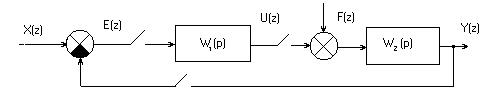
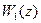 может представлять цифровой
может представлять цифровой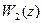 преобразованные в цифровую форму непрерывные элементы системы (объект управления) и устройства связи с объектом управления.
преобразованные в цифровую форму непрерывные элементы системы (объект управления) и устройства связи с объектом управления.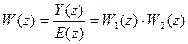
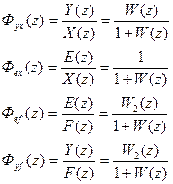

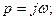

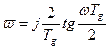
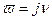
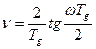 - псевдочастота.
- псевдочастота.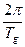 . Иногда удобно пользоваться при анализе и синтезе цифровых систем управления частотными характеристиками монотонного типа, использовав при этом передаточную функцию
. Иногда удобно пользоваться при анализе и синтезе цифровых систем управления частотными характеристиками монотонного типа, использовав при этом передаточную функцию  на
на 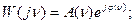
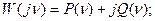
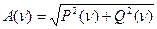 ;
; 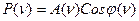 ;
; 
 ; A2.
; A2. 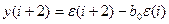
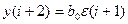 ; А4.
; А4. 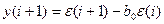
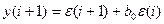 А6.
А6. 
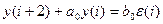 А8.
А8. 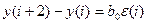
 А10.
А10. 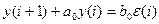
 А12.
А12. 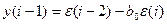
 А14.
А14. 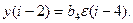
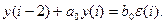 А18.
А18. 
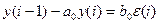 А20.
А20. 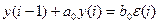
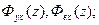
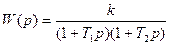 ; Б2.
; Б2. 
 ; Б4.
; Б4. 
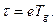
 .
. ; В2.
; В2. 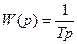 ; В3.
; В3. 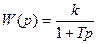 ; В4.
; В4. 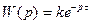 ;
;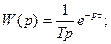 В6.
В6.  В7.
В7.