Устойчивость линейных систем автоматического регулирования.
2.1. Понятие об устойчивости линейных систем регулирования. Необходимые и достаточные условия устойчивости. Дифференциальное уравнение линейной АСР, записанное для регулируемой величины
Коэффициенты Изменение регулируемой величины
представляющем собой сумму свободной и вынужденной составляющих. В соответствии с определением устойчивости данным А.М.Ляпуновым, система будет асимптотически устойчивой, если с течением времени при
Чтобы найти эту составляющую необходимо решить уравнение (1) без правой части, подставив в него решение
то есть
Дифференцируя выражение (4) n раз и подставляя в (5), после сокращения на общий множитель
Полученное алгебраическое уравнение называется характеристическим уравнением. Очевидно, что левые части уравнений (1) и (6) совпадают по форме, поэтому характеристическое уравнение получают обычно, приравнивая к нулю дифференциальный оператор при выходной величине в исходном дифференциальном уравнении (1). Однако в этом случае p означает уже не символ дифференцирования, а некоторое комплексное число. В общем случае Решение характеристического уравнения степени n содержит п корней. Корни при этом могут быть вещественными, комплексными попарно сопряженными, мнимыми попарно сопряженными и нулевыми. Если всего корней n и из них m корней являются вещественными, а остальные комплексными попарно сопряженными, решение можно представить в виде:
где постоянные Для устойчивости линейной системы необходимо и достаточно, чтобы все корни ее характеристического уравнения (6) находились в левой полуплоскости комплексной плоскости. Необходимо пояснить, что корни характеристического уравнения Постоянные Таким образом, для оценки устойчивости линейной системы необходимо определить корни характеристического уравнения, однако вычисление корней осуществляется просто только для уравнений первого и второго порядков. Поэтому весьма важное значение приобретают правила, которые позволяют оценить устойчивость системы без процедуры вычисления корней. Эти правила называются критериями устойчивости. С помощью критериев устойчивости можно не только установить устойчива система или нет, но и выяснить, как влияют на устойчивость те или иные параметры и структурные изменения в системе. 2.2. Критерии устойчивости. Критерии устойчивости разделяются на алгебраические и частотные. Алгебраические критерии устойчивости позволяют судить об устойчивости системы по коэффициентам характеристического уравнения (6). В соответствии с теоремой Безу это уравнение можно представить в виде:
Легко доказать, что для систем первого и второго порядков необходимым и достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения. В этом случае все корни этого уравнения лежат в левой полуплоскости. Для систем третьего и последующих порядков положительность коэффициентов характеристического уравнения является необходимым, но не достаточным условием устойчивости. Оценить устойчивость систем третьего и более высоких порядков позволяют алгебраические критерии устойчивости. 2.2.1. Критерий устойчивости Гурвица. Для оценки устойчивости системы необходимо из коэффициентов характеристического уравнения составить квадратную матрицу, содержащую n-строк и n-столбцов. Определитель Гурвица для уравнения (6) имеет следующий вид:
Правило составления определителя: По главной диагонали определителя слева направо выписываются все коэффициенты характеристического уравнения от Критерий устойчивости Гурвица формулируется следующим образом: Для того, чтобы система автоматического регулирования была устойчива, необходимо и достаточно, чтобы все главные миноры определителя Гурвица были положительны, то есть при
Раскрывая определитель Гурвица для характеристических уравнений первого, второго, третьего и четвертого порядков, можно получить следующие условия устойчивости: - для уравнения первого порядка - для уравнения второго порядка - для уравнения третьего порядка - Для уравнения четвертого порядка Таким образом, необходимым и достаточным условием устойчивости для систем первого и второго порядков является положительность коэффициентов характеристического уравнения. Для уравнений третьего и четвертого порядков кроме положительности коэффициентов необходимо соблюдение дополнительных неравенств. При
2.2.2.Критерий устойчивости Рауса. Воспользуемся этим критерием для оценки устойчивости системы, динамические свойства которой описываются характеристическим уравнением (6). Составим матрицу:
Коэффициенты Другие коэффициенты Из основной матрицы необходимо составить вспомогательные матрицы, имеющие только по две соседних строки основной матрицы:
Миноры каждой из предыдущих матриц, включающие первый столбец, образуют последовательность искомых коэффициентов верхней строки следующей матрицы, то есть:
Для устойчивости линейной системы необходимо и достаточно, чтобы все элементы первого столбца основной матрицы были положительны, то есть:
2.2.3. Частотные критерии устойчивости. Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. 2.2.3.1.Критерий устойчивости Михайлова. Позволяет оценить устойчивость замкнутой системы по виду кривой Михайлова, которая может быть получена из характеристического уравнения замкнутой системы автоматического управления. Если в характеристическое уравнение (6) подставить значение
Для устойчивости замкнутой линейной системы необходимо и достаточно, чтобы кривая Михайлова при изменении частоты от 0 до Кривая Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причем конец ее уходит в бесконечность в том квадранте координатной плоскости, номер которого равен порядку характеристического уравнения. Анализ кривой Михайлова показывает, что при последовательном ее прохождении квадрантов координатной плоскости вещественная и мнимая оси пересекаются ею поочередно. В точках пересечения кривой Михайлова с вещественной осью обращается в нуль мнимая функция Поэтому значения частот, при которых происходит пересечение кривой с вещественной и мнимой осями, должны являться корнями уравнений Эти функции можно представить графически в виде кривых. Точки пересечения этих кривых с осью абсцисс дают значения корней уравнений (9). Отсюда можно сформулировать критерий перемежаемости корней, в соответствии с которым система автоматического управления устойчива тогда и только тогда, когда корни действительной и мнимой частей вектора
2.2.3.2. Критерий устойчивости Найквиста. Этот критерий позволяет оценить устойчивость замкнутой системы по виду амплитудно-фазовой характеристике разомкнутой системы Формулируется критерий Найквиста следующим образом: 1) Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы при изменении частоты от 0 до 2) Неустойчивая разомкнутая система с характеристическим уравнением, имеющим к-корней в правой полуплоскости, будет устойчивой в замкнутом состоянии, если амплитудно-фазовая характеристика разомкнутой системы при возрастании частоты от 0 до Пересечение отрезка действительной оси (-1, - если разомкнутая система неустойчива и ее характеристическое уравнение имеет к-корней в правой полуплоскости, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы число положительных переходов было больше числа отрицательных переходов АФК разомкнутой системы через отрезок действительной оси (-1, - если разомкнутая система астатическая с порядком астатизма равным 1 устойчива, то замкнутая система устойчива тогда и только тогда, когда при изменении частоты
2.3. Структурно-устойчивые и структурно-неустойчивые АСР Структурно-устойчивой АСР называется такая система, которая может быть сделана устойчивой путем выбора параметров - коэффициентов усиления и постоянных времени динамических звеньев. Структурно-неустойчивой АСР называется система, которая неустойчива при любых значениях параметров и которую можно сделать устойчивой лишь при изменении ее структуры. Структурно-устойчивые АСР приведены на рис.2.1а,б.
рис. 2.1а
рис.2.1б Структурно-неустойчивые АСР приведены на рис.2.2а,б
рис.2.2а
рис.2.2б
Наличие в одноконтурной системе консервативного звена (рис.2.2а) или двух интегрирующих звеньев (рис.2.2б) свидетельствует о наличии чисто мнимых корней в характеристическом уравнении, что характеризует незатухающие периодические режимы в системе. Структурно-неустойчивые системы можно перевести в структурно-устойчивые используя местные обратные связи, как это показано на рис.2.3а,б.
рис.2.3а
рис.2.3б
2.4.Выделение областей устойчивости.(Д-разбиение) Критерии устойчивости, рассмотренные ранее, позволяют выяснить устойчива или неустойчива динамическая система. При этом предполагают, что все параметры системы заданы. Однако часто задача ставится таким образом: из всех параметров системы заданы все, кроме одного или двух параметров. Необходимо установить, при каких значениях этого одного параметра или при каких сочетаниях этих двух параметров система будет устойчива. Таким образом, ставится задача выделения области устойчивости по одному или двум параметрам. Впервые эта задача была решена И.А. Вышнеградским. Им была построена область устойчивости в плоскости двух параметров АСР третьего порядка. Характеристическое уравнение АСР третьего порядка в канонической форме имеет следующий вид:
Поделим все члены этого уравнения на
Введем подстановку
Обозначим Таким образом, характеристическое уравнение с учетом обозначений можно представить в виде:
Условие нахождения системы на границе устойчивости АВ-1=0,
На рис.2.4 в плоскости параметров А и В приведены: граница области устойчивости и три подобласти, одна ограничена кривыми ДСЕ, другая - кривыми ЕСР и третья подобласть расположена между границей устойчивости и кривыми ДСР.
рис.2.4.
Если все параметры АСР заданы, то вычислив значения А и В и определив положение точки на плоскости, можно оценить не только устойчивость системы, но и определить вид переходного процесса в системе. Если заданы только параметры объекта управления, а параметры регулятора надо подобрать, исходя из желаемого характера переходного процесса, то на диаграмме необходимо выбрать значения А и В и по ним рассчитать параметры регулятора. В 1948 г. Ю.И.Неймарк разработал общую теорию построения областей устойчивости линейных систем. Этот метод дает возможность построением одной кривой (границы Д-разбиения) сразу определить все те значения интересующего нас параметра, при которых система остается устойчивой. Существо этого метода рассмотрим на примере третьего порядка. Для геометрической интерпретации метода представим характеристическое уравнение системы
В трехмерном пространстве по осям отложим коэффициенты b1,b2,b3.
рис.2.5
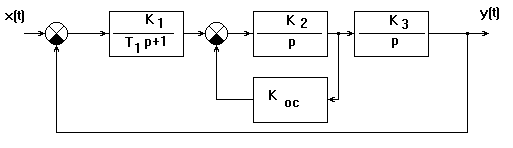
Точке М1 соответствует полином Для системы, представленной на рис.2.6 характеристическое уравнение имеет следующий вид:
рис.2.6 Пусть мы хотим выделить область устойчивости по общему коэффициенту усиления Кобщ=К1К2К3. Решаем характеристическое уравнение относительно Кобщ. Если хотя бы один корень уравнения расположен на мнимой оси, границу Д-разбиения по общему коэффициенту усиления определяем при подстановке
рис.2.7.
На рис.2.7 наиболее вероятной областью устойчивости является 1 область. Ее проверяют на устойчивость при КОБЩ=0 (точка 0). При этом характеристическому уравнению соответствуют три отрицательных корня
|

 при наличии управляющего воздействия x(t)=g(t) имеет вид:
при наличии управляющего воздействия x(t)=g(t) имеет вид: (1)
(1)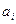 и
и 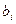 представляют собой постоянные величины, а
представляют собой постоянные величины, а  - оператор дифференцирования.
- оператор дифференцирования.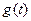 определяется решением уравнения (1):
определяется решением уравнения (1): (2)
(2) , свободная составляющая решения будет стремиться к нулю, т.е.
, свободная составляющая решения будет стремиться к нулю, т.е. (3).
(3).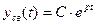 (4)
(4) (5)
(5) получим:
получим: (6).
(6). .
. (7)
(7)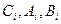 определяются из начальных условий.
определяются из начальных условий. зависят только от вида левой части дифференциального уравнения (1) линейной системы.
зависят только от вида левой части дифференциального уравнения (1) линейной системы.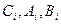 зависят и от правой части этого уравнения, поэтому скорость затухания и форма переходного процесса определяются как левой, так и правой частями исходного уравнения. Однако, поскольку в понятие устойчивости входит только факт наличия или отсутствия затухания переходного процесса, устойчивость линейной системы не зависит от вида правой части дифференциального уравнения (1) и определяется только характеристическим уравнением (6).
зависят и от правой части этого уравнения, поэтому скорость затухания и форма переходного процесса определяются как левой, так и правой частями исходного уравнения. Однако, поскольку в понятие устойчивости входит только факт наличия или отсутствия затухания переходного процесса, устойчивость линейной системы не зависит от вида правой части дифференциального уравнения (1) и определяется только характеристическим уравнением (6). (8)
(8)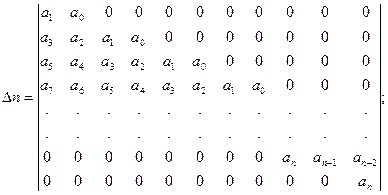
 до
до 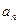 . Вправо от элементов главной диагонали в каждой строке записываются коэффициенты с последовательно убывающими индексами, влево – с последовательно возрастающими индексами. При этом на место коэффициентов с индексами большими n или меньшими 0 записываются нули.
. Вправо от элементов главной диагонали в каждой строке записываются коэффициенты с последовательно убывающими индексами, влево – с последовательно возрастающими индексами. При этом на место коэффициентов с индексами большими n или меньшими 0 записываются нули.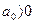 для устойчивости системы необходимо и достаточно выполнение следующих условий:
для устойчивости системы необходимо и достаточно выполнение следующих условий: и т.д.
и т.д. , условие устойчивости
, условие устойчивости 
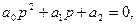 условие устойчивости
условие устойчивости 
 .
. , условия устойчивости
, условия устойчивости  .
. , условия устойчивости
, условия устойчивости  ;
; 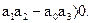
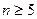 число дополнительных неравенств возрастает и процесс раскрытия определителей становится трудоемким. Поэтому критерий Гурвица обычно применяют при
число дополнительных неравенств возрастает и процесс раскрытия определителей становится трудоемким. Поэтому критерий Гурвица обычно применяют при 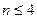 . При порядке уравнения больше четырех удобнее пользоваться другими критериями, например критерием Рауса.
. При порядке уравнения больше четырех удобнее пользоваться другими критериями, например критерием Рауса.
 вычисляются по рекуррентным формулам.
вычисляются по рекуррентным формулам. ;
;  ;
;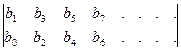 ;
;  ;
;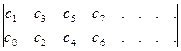 ;
;  ;
; .
.
 и т.д.
и т.д. и т.д.
и т.д. , то получим комплексный полином
, то получим комплексный полином , где
, где  и
и 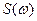 - полиномы соответственно четных и нечетных степеней относительно
- полиномы соответственно четных и нечетных степеней относительно 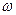 . При изменении частоты
. При изменении частоты  вектор
вектор  , изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости некоторую кривую, называемую кривой Михайлова. Критерий Михайлова формулируется следующим образом:
, изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости некоторую кривую, называемую кривой Михайлова. Критерий Михайлова формулируется следующим образом: на вещественной положительной полуоси, обходила против часовой стрелки последовательно n-квадрантов (n – порядок характеристического уравнения), нигде не обращаясь в нуль.
на вещественной положительной полуоси, обходила против часовой стрелки последовательно n-квадрантов (n – порядок характеристического уравнения), нигде не обращаясь в нуль.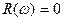 и
и  (9).
(9). раз.
раз. на
на  (по часовой стрелке) не охватывает точку с координатами (-1,j0).
(по часовой стрелке) не охватывает точку с координатами (-1,j0).





 , при этом получим
, при этом получим
 , тогда плучим:
, тогда плучим: 

 , где А и В - параметры Вышнеградского.
, где А и В - параметры Вышнеградского.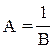 - гипербола Вышнеградского.
- гипербола Вышнеградского.
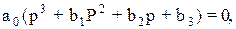 где
где 

 , а точке М2 - полином
, а точке М2 - полином 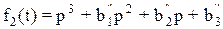 . Когда р принимает значение корня, полином обращается в нуль. Поэтому корни уравнения называют нулями полинома. Каждой точке трехмерного пространства будет соответствовать три точки на плоскости корней. При переходе от точки к точке в пространстве полиномов на плоскости корней, будет изменяться расположение нулей. Зная расположение нулей можно ответить на вопрос, устойчива или неустойчива система.
. Когда р принимает значение корня, полином обращается в нуль. Поэтому корни уравнения называют нулями полинома. Каждой точке трехмерного пространства будет соответствовать три точки на плоскости корней. При переходе от точки к точке в пространстве полиномов на плоскости корней, будет изменяться расположение нулей. Зная расположение нулей можно ответить на вопрос, устойчива или неустойчива система.

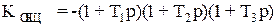 .
. т.е.
т.е.  при изменении частоты
при изменении частоты 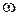 от
от  до
до  на комплексной плоскости КОБШ выделяется область соответствующая комплексной области корней характеристического уравнения, причем граница мнимой оси этой плоскости отображается штриховкой. Штриховка направлена внутрь области соответствующей левым корням характеристического уравнения.
на комплексной плоскости КОБШ выделяется область соответствующая комплексной области корней характеристического уравнения, причем граница мнимой оси этой плоскости отображается штриховкой. Штриховка направлена внутрь области соответствующей левым корням характеристического уравнения.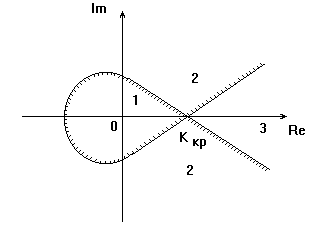
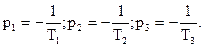 Все точки области 1 соответствуют устойчивости системы. Таким образом, отрезок вещественной оси от нуля до ККР определяет численные значения КОБЩ, при которых система устойчива.
Все точки области 1 соответствуют устойчивости системы. Таким образом, отрезок вещественной оси от нуля до ККР определяет численные значения КОБЩ, при которых система устойчива.


