ТИПОВАЯ ЗАДАЧА
Задача:
Разработать способ оценки работы филиалов промышленного предприятия с использованием метода экспертных оценок.
Решение:
Выберем предварительную группу из 20 экспертов по 4 из человека из сферы: экономики, производства, высшего образования, менеджмента. При выборе будем учитывать следующие критерии: - компетентность потенциального эксперта в технологии экономических особенностях производства и сбыта продукта, изготавливаемого филиалами предприятия; - эрудированность в области производства и реализации схожей продукции; - участие в подобных исследованиях в прошлом.
Проведём общее собрание предварительной группы, где предложим экспертам выделить показатели деятельности филиалов, по которым следует делать выводы о качестве работы филиала. Заседание проводим методом «мозговой штурм». В результате заседания были предложены 5 показателей: - рентабельность активов; - автономность филиала; - комплексный показатель качества продукции; - темпы роста спроса на продукцию филиала; - текучесть персонала.
На данном этапе, мы не можем сравнивать эти показатели между собой. Поясним это на примере. Если рентабельность одного филиала в сравнении с другим выше в 3 раза, а автономность ниже на 0,1%, то очевидно, что для данного случая рентабельность активов более весомо влияет на оценку работы филиала. Предположим другой пример автономность одного филиала в 3 раза выше автономности другого, при том, что рентабельность ниже на 0,1%. В этой ситуации наоборот приоритет при оценке работы филиала следует отдать показателю автономности. Таким образом, для того чтобы показатели можно было корректно сравнивать необходимо количественно уточнить предложенные показатели. Проведём закрытые заседания представителей от каждой сферы, где предложим выбрать по одному представителю для участия в рабочей группе. Далее проведём общее собрание предварительной группы и предложим выбрать ещё 2х экспертов из тех, кто не оказался в числе уже выбранных представителей или из числа специалистов, которые не были приглашены в предварительную группу, но по мнению группы достойны того, чтобы давать экспертные оценки по предложенной нам задаче. Таким образом, сформирована рабочая группа из 6-ти экспертов. Рабочей группе предложим количественно дополнить, предложенные предварительной группой показатели. В результате работы рабочей группы, было предложено сравнивать следующие показатели: - рентабельности активов на 10% выше средней по предприятию; - отклонение автономности на 10% от среднего по предприятию; - комплексный показатель качества продукции на 5% выше среднего по предприятию; - темпы роста спроса на продукцию филиала на 5% выше среднего по предприятию; - текучесть персонала на 15% выше, чем в среднем по предприятию.
Предлагаем экспертам, вошедшим в рабочую группу неделю посвятить изучению влияния каждого из 5-ти предложенных показателей на выявление качества работы филиала. По прошествии недели, каждому эксперту рабочей группы предлагаем анонимную анкету, где он может оценить каждый показатель по шкале от 1-ого до 5-ти, где 5 – означает наибольшее влияние показателя на оценку результатов работы. В результате опроса были получены оценки, представленные в таблице 2.1. Проранжируем оценки, представленные в таблице 2.1, выставляя ранг 5 наибольшим оценкам и 1 – наименьшим. Первый и четвёртый эксперты выставил оценки от 1-ого до пяти, не допуская повторения оценок различным факторам, поэтому их оценки одновременно являются и рангами. Таблица 2.1 – Оценки экспертов рабочей группы
Второй, третий и шестой эксперт допустили одинаковые оценки по двум факторам, поэтому их ранги рассчитываем по средней тех мест, которые делят между собой факторы. Так у второго эксперта факторы №2 и №5 получили наименьшую оценку, следовательно, они делят между собой ранги 1 и 2. В среднем это соответствует числу 1,5. У третьего же эксперта одинаковые оценки получили факторы №1 и №4. На первом месте тут фактор №3, который получает ранг - 5, факторы с номером 1 и 4 делят второе и третье место, за которые полагается соответственно 4 и 3 балла. В среднем это получается 3,5. Пятый эксперт выставил одинаковую максимальную оценку трём факторам, следовательно, они делят между собой ранги 5,4,3. В среднем это соответствует числу 4. Обратим внимание, что у эксперта №6 третье место занимает фактор №3 с оценкой 2. Вне зависимости от того, какая оценка, раз этот фактор занял третье место, он получает 3-тий по шкале (5,4,3,2,1) по величине ранг – 3.
Таблица 2.2 – Таблица рангов факторов
Обратим внимание, что сумма рангов по каждому эксперту одинакова – 15. Действительно ведь для каждого эксперта мы распределяли ранги 5,4,3,2,1, что в сумме даёт 15. Рассчитаем величину согласованности для этого сложим ранги по каждому фактору, найдём среднюю от полученных сумм и рассчитаем сумму квадратов разниц полученных сумм от их средней (см. формулу 1.6).
Таблица 2.3 – Расчёт согласованности экспертов
Рассчитаем максимальную согласованность экспертов по формуле 1.11. Для этого посчитаем сколько раз эксперты выставляли одинаковые ранги разным факторам (таблица 2.2). Первый и четвёртый эксперт не выставляли одинаковые ранги, второй, третий и шестой эксперт по одному разу выставили одинаковые ранги (3 пары одинаковых рангов). Пятый эксперт выставил одну тройку одинаковых рангов. Таким образом, в нашей повторяющихся рангов.
Согласованность у наших экспертов равна 257,5 при максимальной согласованности 339. Следовательно, относительная согласованность, рассчитанная на основе коэффициента конкордации Кендела (1.12) равна 0,76
Проверим, достаточна ли данная величина согласованности, чтобы принимать решения по критерию χ2 Пирсона (см. формулу 1.13), который равен 18,24
Сравним расчётный показатель с табличным (Приложение В, таблица В.2) при степени достоверности 95% (вероятности шибки = 5%). Табличный показатель Пирсона с 4-мя степенями свободы и 5% вероятности ошибиться равен 9,5. Расчётный показатель (18,24) больше чем табличный (9,5), следовательно, коэффициенту конкордации Кендела доверять можно, а раз сам этот коэффициент больше 0,7 (0,76), то между экспертами существует достаточный уровень согласованности и на основе их оценок можно принимать решения. Принимать решение удобнее, когда информация для принятия решений представлена в графическом виде. Построим диаграмму сумм рангов, которые набрал каждый из факторов.
Рисунок 2.1 – Сила влияния факторов на оценку работы филиалов предприятия
Как можно увидеть на графике, наибольшее влияние на оценку работы филиалов оказывает первый фактор - рентабельности активов на 10% выше средней по предприятию, его сумма рангов - 26,5. Наименьшее влияние наблюдается у пятого фактора - текучесть персонала на 15% выше, чем в среднем по предприятию, у него сумма рангов – 8, что в 3,3 раз меньше, чем у первого фактора. Таким образом, в ходе анализа экспертных оценок мы не только определили наиболее значимые показатели оценки работы филиала, но и выявили количественные величины превалирования одного фактора над другим, которые соответствуют суммам рангов каждого фактора. Эти количественные величины мы и будем использовать в оценке работы филиалов. При этом, если за 10 % прироста рентабельности полагается 26,5 баллов, то для 20% прироста этому показателю будет присвоено 53 балла (26,5*2). Приведём пример оценки работы филиалов, для этого возьмём данные по 4-м филиалам предприятия и рассчитаем средние величины рассматриваемых показателей (таблица 2.4). Рассчитаем прирост показателей относительно их средней величины (таблица 2.5). Сравним полученные величины с выбранными для сравнения (10% для первых двух показателей, 5% для третьего и четвёртого, 15% для последнего показателя) Найдём отношение прироста показателей к выбранным для сравнения величинам (таблица 2.6). Умножим каждое из полученных значений на баллы, выставляемые на основе полученных сумм рангов (таблица 2.7).
Таблица 2.4 – Данные о величине показателей по филиалам предприятия
Таблица 2.5 – Прирост показателей относительно средней величины по предприятию
Таблица 2.6 – Отношение прироста показателей к выбранным для сравнения величинам
Таблица 2.7 – Количество баллов, набранных каждым филиалом
В данном примере, среди филиалов наилучшая работа наблюдается у филиала №2 – 102,55 баллов, наихудшая работа наблюдается в филиале №1 – минус 115,5 баллов
Таким образом, мы можем предложить предприятию следующую формулу для оценки качества работы филиала:
где Качф – показатель качества работы филиала; Хф – сумма рангов по выбранному фактору; Пф,i – фактическая величина прироста i-того показателя; Пв,i – выбранная величина прироста i-того показателя; n – количество показателей.
Выбранные для сравнения величины прироста (Пв,i) для каждого показателя были определены на предварительном этапе анализа экспертных оценок и составили:
Таблица 2.8 – Сумма рангов за прирост показателей
Фактические величины прироста показателей (Пф,i) представляют из себя отношение фактических данных к их средней величине по всем филиалам.
где Фp – величина фактора для p-того филиала; m – количество филиалов.
Таким образом, в ходе анализа экспертных оценок предприятию была предложена модель оценки качества работы филиалов. Эта модель представлена формулами 2.4, 2.5 и данными из таблицы 2.8
|




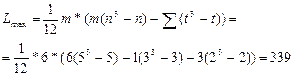 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3)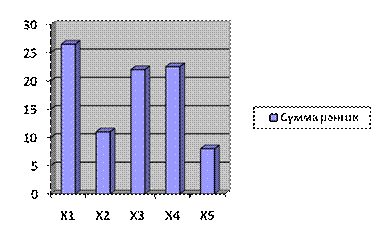
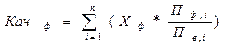 , (2.4)
, (2.4)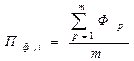 , (2.5)
, (2.5)


