Показатели согласованности экспертов
Чем более согласованны эксперты, тем более далеки друг от друга суммы рангов, по каждому фактору.
Например, три эксперта дают оценки пяти факторам. Если все эксперты дали первому фактору максимальный ранг – 1, а второму фактору минимальный ранг – 5, то сумма рангов по первому фактору будет равна 3 (1 ранг * 3 эксперта), а сумма рангов по второму фактору равна 15 (5 ранг * 3 эксперта). Таким образом, разница сумм будет равна 15-3=12
Если эксперты разойдутся во мнениях, и первому фактору реже будут присваивать первый ранг, то сумма рангов по первому фактору станет больше чем 3 и приблизиться к сумме рангов второго фактора (равного 15-ти). Аналогично, если эксперты разойдутся в мнениях и второму фактору будут давать не последние ранги (ставить меньше 5-ого ранга), то сумма рангов по данному фактору сократится и приблизится к сумме рангов первого фактора (равного 3-м). В нашем примере, разница составила 13-6=7.
Таким образом, согласованность экспертов возрастает по мере возрастания разницы между суммами рангов по разным факторам. Сложив все разницы между суммами рангов факторов можно найти общую величину согласованности экспертов. Чтобы избавиться от влияния на сумму отрицательных разниц, следует искать сумму квадратов разниц между накопленными рангами.
Для упрощения дальнейших преобразований введём допущения: 1) В сумму квадратов разниц включим по паре квадратов разниц между каждым фактором (Ха-Хв)2 и (Хв-Ха)2, в результате этого результат (S) увеличится в два раза (2*S), позднее мы разделим результат пополам и снимем данное допущение; 2) В сумму включим разницы между каждым фактором с самим собой (Ха-Ха)2, на конечный результат эти разницы не повлияют, так как равны нулю, однако значительно облегчат дальнейшие расчёты.
Извлечём квадраты:
Раскроем скобки, перегруппируем элементы:
Продолжим преобразование:
Вынесем за скобки одинаковые члены уравнения:
Снимем первое допущение и получим вполне удобную формулу для расчёта показателя согласованности экспертов:
Данную формулу можно немного преобразовать:
Вынесем «n» за скобки и сведём выражение в скобках к формуле разности квадратов:
Заметим, что в результате мы получаем формулу суммы квадратов отклонений накопленных рангов от их средней величины, умноженной на «n». Эта формула и будет базовой для всех наших последующих расчётов.
ПРИЛОЖЕНИЕ Б
|

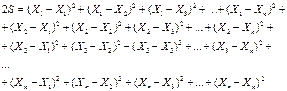 , (А.1)
, (А.1) , (А.2)
, (А.2) , (А.3)
, (А.3) , (А.4)
, (А.4)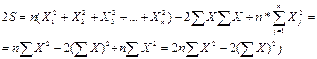 , (А.5)
, (А.5) , (А.6)
, (А.6)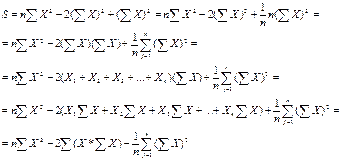 , (А.7)
, (А.7)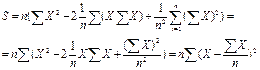 , (А.8)
, (А.8) , (А.9)
, (А.9)


