Выведение формулы максимальной величины согласованности экспертов
Максимальная согласованность возникает тогда, когда все эксперты дали одинаковые ранги одним и тем же факторам.
| Факторы
| Эксперт 1
| Эксперт 2
| …
| Эксперт m
| | Х1
|
|
| …
|
| | Х2
|
|
| …
|
| | Х3
|
|
| …
|
| | …
| …
| …
| …
| …
| | Хn
| n
| n
| n
| n
|
Попробуем рассчитать максимальную согласованность экспертов для n факторов и m экспертов. Воспользуемся для этого формулой:
 , (Б.1) , (Б.1)
Подставим ранги. Так как при максимальной согласованности экспертов мнения экспертов по каждому фактору – совпадают, следовательно совпадают и ранги факторов. Посчитаем сумму рангов каждого фактора. С учётом того, что ранги всех экспертов по каждому фактору совпадают, то сумма рангов каждого фактора будет равна произведению величины ранга по данному фактору на количество экспертов.
| Факторы
| Эксперт 1
| Эксперт 2
| …
| Эксперт m
| Σ рангов
М
| | Х1
|
|
| …
|
| 1*m
| | Х2
|
|
| …
|
| 2*m
| | Х3
|
|
| …
|
| 3*m
| | …
| …
| …
| …
| …
| …
| | Хn
| N
| n
| n
| n
| n*m
|
Для расчёта максимальной согласованности по формуле Б.1 нам ещё понадобиться рассчитать среднюю сумм рангов.
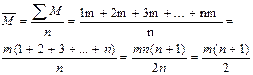 , (Б.2) , (Б.2)
Теперь рассчитаем квадрат разницы суммы рангов каждого фактора от средней суммы рангов
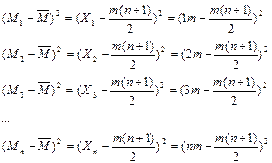 , (Б.3) , (Б.3)
Упростим полученные формулы:
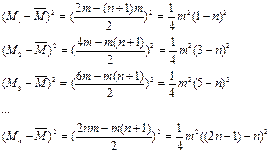 , (Б.4) , (Б.4)
Продолжим преобразование:
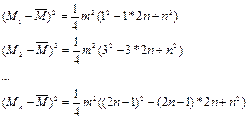 , (Б.5) , (Б.5)
Рассчитаем максимальную согласованность по формуле Б.1:
 , (Б.6) , (Б.6)
Таким образом, максимальная согласованность может быть определена по формуле:
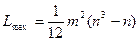 , (Б.7) , (Б.7)
Проверим полученную формулу для случая с 3мя экспертами и 4-мя факторами, для этого составим таблицу с согласованными оценками экспертов и сравним рассчитанную по таблице согласованность с расчётом по формуле Б.7
| Фактор
| Эксперт №1
| Эксперт №2
| Эксперт №3
| Σ рангов (M)
| M – Mср
| L
| | Х1
|
|
|
| 3
| -4,5
| 20,25
| | Х2
|
|
|
| 6
| -1,5
| 2,25
| | Х3
|
|
|
| 9
| 1,5
| 2,25
| | Х4
|
|
|
| 12
| 4,5
| 20,25
| | Всего
| 10
| 10
| 10
| 30
|
|
|
 , (Б.8) , (Б.8)
Действительно для случая с 3-мя экспертами и 4-мя факторами максимальная согласованность, рассчитанная по формуле Б.7 совпадает с согласованностью рассчитанной таблично.
Проверим, полученную формулу для того же случая при условии, что полностью согласованные эксперты одной паре факторов дадут одинаковые ранги.
| Фактор
| Эксперт №1
| Эксперт №2
| Эксперт 3
| Σ рангов
| M – Mср
| L
| | Х1
| 1,5
| 1,5
| 1,5
| 4,5
| -3
|
| | Х2
| 1,5
| 1,5
| 1,5
| 4,5
| -3
|
| | Х3
|
|
|
| 9
| 1,5
| 2,25
| | Х4
|
|
|
| 12
| 4,5
| 20,25
| | Всего
| 10
| 10
| 10
| 30
|
| 40,5
|
Результат расчётов показал, что полученная нами формула, показывает максимальную согласованность экспертов лишь при условии, что эксперты не ставят одинаковых оценок разным факторам. Если эксперты допускают единые оценки, необходимо уменьшить величину максимальной согласованности на некий добавочный компонент.
Такой добавочный компонент, для пары одинаковых рангов можно найти по формуле:
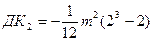 , (Б.9) , (Б.9)
Проверим дополнительный компонент на нашем примере:
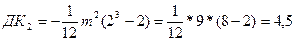 , (Б.10) , (Б.10)
Действительно, максимальное согласование экспертов при наличии одной пары одинаковых оценок у каждого из экспертов равняется 45-40,5 = 4,5. С учётом того, что таких пар в нашем случае – 3 (у каждого эксперта по одной), то на каждую пару добавочный компонент = 4,5/3=1,5
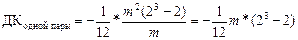 , (Б.11) , (Б.11)
Аналогично мы можем определить, что добавочный компонент трёх одинаковых рангов, будет определяться по формуле:
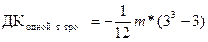 , (Б.12) , (Б.12)
Для произвольного случая добавочный коэффициент равен сумму добавочных компонентов для каждой встречающейся пары, тройки и т.д. значений.
 , (Б.13) , (Б.13)
где ДК – добавочный коэффициент максимальной согласованности
R – количество случаев, когда эксперты давали одинаковые ранги разным факторам
ti – количество факторов, получивших одинаковые оценки в i-том случае.
ПРИЛОЖЕНИЕ В
| Степени свободы K
| Вероятность
| | 0,99
| 0,98
| 0,95
| 0,90
| 0,70
| 0,50
| |
| 0,00016
| 0,0006
| 0,0039
| 0,016
| 0,148
| 0,455
| |
| 0,020
| 0,04
| 0,103
| 0,211
| 0,713
| 1,386
| |
| 0,115
| 0,185
| 0,352
|
| 1,424
| 2,366
| |
| 0,30
| 0,43
| 0,71
| 1,06
| 2,19
| 3,36
| |
| 0,55
| 0,75
| 1,14
| 1,61
| 3,00
| 4,35
| |
| 0,187
| 1,13
| 1,63
| 2,20
| 3,83
| 5,35
| |
| 1,24
| 1,56
| 2,17
| 2,83
| 4,67
| 6,34
| |
| 1,65
| 2,03
| 2,73
| 3,49
| 5,53
| 7,34
| |
| 2,09
| 2,53
| 3,32
| 4,17
| 6,39
| 8,35
| |
| 2,56
| 3,06
| 3,94
| 4,86
| 7,27
| 9,34
| Таблица В.1 - Значение c2 и числа степеней свободы K
| Степени свободы K
| Вероятность ошибиться
| | 0,30
| 0,20
| 0,10
| 0,05
| 0,02
| 0,01
| |
| 1,07
| 1,64
| 2,7
| 3,8
| 5,4
| 6,6
| |
| 2,41
| 3,22
| 4,6
| 6,0
| 7,8
| 9,2
| |
| 3,66
| 4,64
| 6,3
| 7,8
| 9,8
| 11,3
| |
| 4,9
| 6,0
| 7,8
| 9,5
| 11,7
| 13,3
| |
| 6,1
| 7,3
| 9,2
| 11,1
| 13,4
| 15,1
| |
| 7,2
| 8,6
| 10,6
| 12,6
| 15,0
| 16,8
| |
| 8,4
| 9,8
| 12,0
| 14,1
| 16,6
| 18,5
| |
| 9,5
| 11,0
| 13,4
| 15,5
| 18,2
| 20,1
| |
| 10,7
| 12,2
| 14,7
| 16,9
| 19,7
| 21,7
| |
| 11,8
| 13,4
| 16,0
| 18,3
| 21,2
| 23,2
| Таблица В.2 - Значение c2 и числа степеней свободы K
ПРИЛОЖЕНИЕ Г
Варианты заданий для студентов
Задание выбирается по последнему номеру зачётной книжки (индивидуального учебного плана)
| №
| Задание
| |
| Выявить наиболее сильных конкурентов и разработать метод их определения в будущем
| |
| Разработать модель определения качества продукции предприятия.
| |
| Разработать способ выбора наиболее привлекательного инвестиционного проекта.
| |
| Определить критерии выбора персонала для предприятия.
| |
| Составить модель выбора производственной линии.
| |
| Разработать модель принятия решения о предоставлении кредита клиенту.
| |
| Разработайте способ выбора банка для депозита денежных средств.
| |
| Предложите методику выбора рекламного проекта для бизнеса предприятия.
| |
| Разработайте способ выбора поставщика ресурсов для предприятия.
| |
| Предложить способ выбора делового партнёра, с которым следует создавать совместный бизнес-проект.
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Типология суицида. Феномен суицида (самоубийство или попытка самоубийства) чаще всего связывается с представлением о психологическом кризисе личности...
ОСНОВНЫЕ ТИПЫ МОЗГА ПОЗВОНОЧНЫХ Ихтиопсидный тип мозга характерен для низших позвоночных - рыб и амфибий...
Принципы, критерии и методы оценки и аттестации персонала
Аттестация персонала является одной их важнейших функций управления персоналом...
|
Условия приобретения статуса индивидуального предпринимателя. В соответствии с п. 1 ст. 23 ГК РФ гражданин вправе заниматься предпринимательской деятельностью без образования юридического лица с момента государственной регистрации в качестве индивидуального предпринимателя. Каковы же условия такой регистрации и...
Седалищно-прямокишечная ямка Седалищно-прямокишечная (анальная) ямка, fossa ischiorectalis (ischioanalis) – это парное углубление в области промежности, находящееся по бокам от конечного отдела прямой кишки и седалищных бугров, заполненное жировой клетчаткой, сосудами, нервами и...
Основные структурные физиотерапевтические подразделения Физиотерапевтическое подразделение является одним из структурных подразделений лечебно-профилактического учреждения, которое предназначено для оказания физиотерапевтической помощи...
|
|

 , (Б.1)
, (Б.1)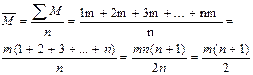 , (Б.2)
, (Б.2)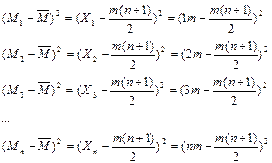 , (Б.3)
, (Б.3)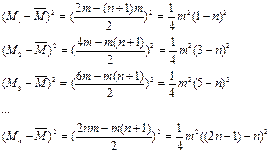 , (Б.4)
, (Б.4)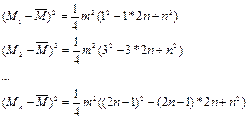 , (Б.5)
, (Б.5) , (Б.6)
, (Б.6)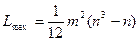 , (Б.7)
, (Б.7) , (Б.8)
, (Б.8)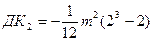 , (Б.9)
, (Б.9)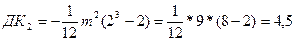 , (Б.10)
, (Б.10)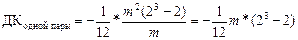 , (Б.11)
, (Б.11)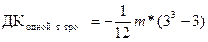 , (Б.12)
, (Б.12) , (Б.13)
, (Б.13)


