Выявление согласованности экспертов
Невозможно сделать обоснованный выбор на основании оценок экспертов, которые совершенно не согласованны (противоречивы) между собой. С одной стороны, полная согласованность экспертов вызывает подозрение в сговоре экспертов или в том, что один из экспертов смог своим авторитетом или инициативностью (что характерно для очных форм опроса) навязать всем единое мнение. С другой стороны, большая несогласованность экспертов создаёт проблему выбора между решениями, которые одни эксперты считают верными, а другие – совершенно неподходящими.
Согласованность экспертов определяется по формуле 1.3, как получена эта формула вы можете ознакомиться в Приложении А.
где S – величина согласованности; n – количество факторов; Xi - сумма рангов экспертов по i-тому фактору;
Величина согласованности, рассчитанная по данной формуле имеет своим недостатком различную максимальную величину данного показателя для анализа при различном количестве экспертов и факторов. Это не трудно заметить, если внимательно посмотреть на формулу 1.3. При увеличении количества экспертов увеличивается первые множитель n и увеличивается количество слагаемых во втором множителе (сумме квадратов разниц суммы рангов от средней суммы рангов). Поэтому, для каждого исследования необходимо знать максимальную величину согласованности, что позволит определить согласованность экспертов в относительных величинах (конкордации):
где W – коэффициент конкордации Кендела; Х – фактические величины накопленных рангов; M – величины накопленных рангов при полной согласованности экспертов
Как мы можем заметить, при расчёте относительной величины согласованности (коэффициент конкордации W), в формулах сократился показатель n, следовательно, при расчёте максимальной и фактической величины согласованности можно его также сократить. Чтобы не запутаться введём новую переменную L:
Теперь формула коэффициента согласованности (конкордации) примет вид:
Максимальная согласованность может быть определена по формуле 1.8 (как была выведена эта формула можете ознакомиться в приложении Б):
где m – количество экспертов.
В случае, если эксперты нескольким факторам дали одинаковые ранги, то величину максимальной согласованности надо откорректировать на добавочный коэффициент максимальной согласованности (ДК). Формула для расчёта этого коэффициента приведена в 2.14 (как была выведена эта формула можете ознакомиться в приложении Б):
где ДК – добавочный коэффициент максимальной согласованности R – количество случаев, когда эксперты давали одинаковые ранги разным факторам ti – количество факторов, получивших одинаковые оценки в i-том случае.
Таким образом, максимальная согласованность экспертов для n факторов, m экспертов и произвольного количества одинаковых оценок, можно определить по формуле:
или
Таким образом, коэффициент конкордации Кендела (относительная величина согласованности) определяется по формуле 1.12
Если W>0,9, то мнения экспертов очень сильно согласованы (возможен сговор экспертов). Если 0,9>W>0,7, то мнения экспертов согласованы. Если 0,7>W>0,5, то мнения экспертов слабо согласованы.Если 0,5>W, то мнения экспертов не согласованы. 1.6 Проверка согласованность W на нулевую гипотезу с помощью χ2 - критерия Пирсона
Когда мы определили согласованность экспертов в относительных величинах W (по формуле 1.12), перед нами стоит задача определить можно ли доверять этому показателю, не явился ли он следствием случайных отетов экспертов. Проверим коэффициент конкордации Кендела с помощью χ2 критерий Пирсона, рассчитанного по формуле 1.13 с табличным значением этого показателя (см. Приложение В, таблицы В.1, В.2).
где K – количество степеней свободы равное «n-1»
Доверять коэффициенту конкордации Кендела W стоит лишь тогда, когда расчётное значение χ2 - критерия Пирсона превысит критическое значением, взятое из таблицы.
|

 , (1.3)
, (1.3) - средняя сумма рангов экспертов.
- средняя сумма рангов экспертов.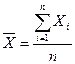 , (1.4)
, (1.4)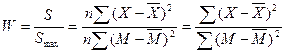 , (1.5)
, (1.5)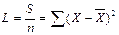 , (1.6)
, (1.6)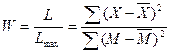 , (1.7)
, (1.7) , (1.8)
, (1.8)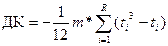 , (1.9)
, (1.9) , (1.10)
, (1.10)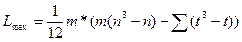 , (1.11)
, (1.11)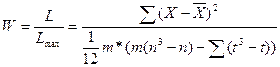 , (1.12)
, (1.12)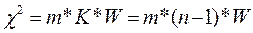 ,(1.13)
,(1.13)


