Визначення показника заломлення із порядкових чисел m
Будемо вважати, що m - не являється дискретно - порядковим числом, а неперервною математичною змінною. Спектр для нормального падіння можна змістити до більш коротких довжин хвиль, якщо збільшити кожне порядкове число на величину ∆т, де ∆m може відрізнятися для кожного т. Зміщення, яке пояснюється косим падінням випромінювання згідно рівняння (2.4), можна виразити через нормальне падіння:
Із рівняння (2.4) і (2.5) і закона Снелліуса випливає, що:
При розгляді двох сусідніх екстремальних значень спектра нормального падіння при довжинах хвиль λ01 λ02 із рівняння (2.3) слідує, що:
Величина М визначається як:
де М > m1.
Рівність М =m1 правильна тільки при відсутності дисперсії. Вплив дисперсії на М можна приблизно визначити математичною функцією типу:
Перший доданок у рівнянні (2.9) відображає відношення 1/λ між т і λ згідно рівняння (2.3), в той час як доданок в дужках приблизно виражає вплив дисперсії. Значення т при кожному екстремальному значенні можна приблизно представити як:
Рівняння (2.9) можна записати у вигляді прямої лінії:
Значення y можна визначити повторенням у і здійсненням лінійної регресії рівняння (2.11). Значення у вибирають таке, щоб воно добре підходило до рівняння (2.11) і давало значення т по наближенню до (2.10), яке відрізняється на 1/2 і також дають правильні, приблизно цілі, значення для кожної екстремальної величини. Із наближених значень т, враховуючи (2.10), точні порядкові числа можна задавати кожній екстремальній величині. Якщо взяти, що п - постійна в області між кожним λ i і дві її сусідні екстремальні величини з нормальним падінням λ01 і λ02, то ∆m можна приблизно визначити по формулі[12]:
Апроксимація (2.12) дає значення
де A=4ad2, B=4bd2.
Оскільки порядкові числа відомі, значення х можна визначити за допомогою лінійної регресії рівняння (2.13). Значення х вибирається таке щоб найкраще підходило екстремальним значенням, а регресія також дає значення А і В. Підстановка рівняння (2.2) у рівняння (2.5), використовуючи рівняння (2.13) для ∆m дає наступний вираз[12]:
Значення ni при кожному значенні λi, можна тепер визначити використовуючи рівняння (2.6), (2.7) і (2.14). Значення d можна визначити, якщо врахувати той факт, що т збільшується на 1/2 для кожної наступної екстремальної величини, яка описана у рівнянні (2.5). Якщо m i - порядкове число першої екстремальної величини, то рівняння (2.5) для наступних екстремальних величин можна записати як [11]:
де l=0,1,2,3,…
Рівняння (2.15) можна графічно зобразити, як це показано на рис.2.2. Пряма лінія через mi, і інші точки має нахил 2d, а значення d можна дістати із цього нахилу. Якщо d відоме, а і b можна визначити із рівняння (2.13), яке завершує обрахунок п'яти сталих.
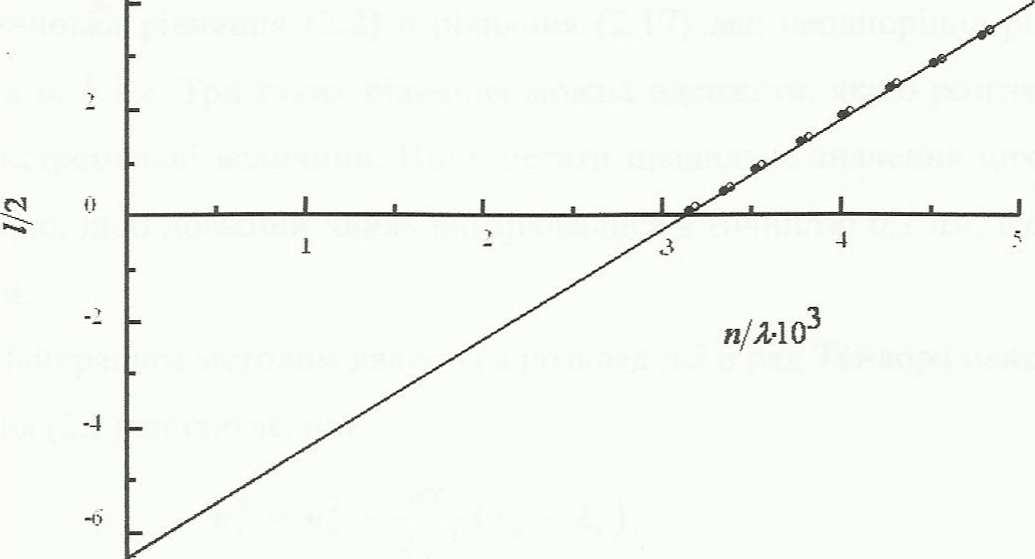
Рис.2.2.Графік залежності пі/λi, від l/2 +∆m (°) і n0 /λ0 від l /2 (•) для визначення товщини плівки d [11].
|

 (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7)
 (2.8)
(2.8)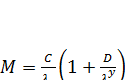 . (2.9)
. (2.9) (2.10)
(2.10) (2.11)
(2.11) (2.12)
(2.12)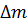 , які на декілька відсотків більші, тому краще скористатися формулою (2.14) [12]. Підставивши рівняння (2.2) у рівняння (2.3) дає
, які на декілька відсотків більші, тому краще скористатися формулою (2.14) [12]. Підставивши рівняння (2.2) у рівняння (2.3) дає (2.13)
(2.13)
 (2.14)
(2.14) (2.15)
(2.15)


