Визначення показника заломлення із рівняння дисперсії
Розглянемо альтернативний спосіб визначення n незалежно від порядкових чисел т. Із рівняння (2.3) і (2.4) випливає
У недисперсній області рівняння (2.16) має вигляд
і n можна визначити безпосередньо із рівняння (2.7). Рівняння (2.16) можна записати, як:
Підстановка рівняння (2.7) у вищезгадане рівняння дає:
а підстановка рівняння (2.2) у рівняння (2.17) дає неоднорідне рівняння в змінних a,bi х. Три таких рівняння можна одержати, якщо розглянути три різні екстремальні величини і a,b,х,можна одержати із цих рівнянь. Щоб дістати правильне значення цих змінних необхідно, щоб довжини хвиль вимірювалися з точністю ̴ 0,1 нм, що нелегко зробити. Кращим методом являється розклад ni2 у ряд Тейлора навколо n0. Із рівняння (2.2) випливає, що:
Підстановка рівняння (2.17) у рівняння (2.18) дає[12]:
де
Рівняння (2.2) і (2.19) показують, що N2 можна представити як функцію виду:
Із рівняння (2.17), (2.19), і (2.21) випливає, що:
х можна визначити обчисленням N2 для кожної екстремальної величини і повторенням х для того, щоб дістати хорошу відповідність (2.21). Ця регресія також дає значення Е, b. Значення а можна визначити із рівняння (2.22) і трьох постійних у рівнянні (2.2). Таким чином визначається дисперсія показника заломлення. Щоб дістати т і d із рівняння, аналогічно рівнянню (2.15), можна записати[12]:
На рис.2.2 зображено графік залежності значень
|

 (2.16)
(2.16)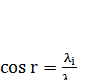 ,
, .
.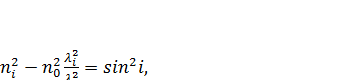 (2.17)
(2.17)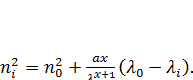 (2.18)
(2.18) (2.19)
(2.19)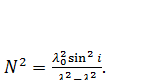 (2.20)
(2.20) (2.21)
(2.21)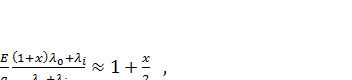 (2.22)
(2.22)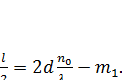 (2.23)
(2.23) від
від  . Екстраполяція прямої лінії через ці точки покаже порядкове число першої екстремальної величини m1. Пряма лінія через т1 та інші точки, мають нахил 2d, із якої можна визначити d.
. Екстраполяція прямої лінії через ці точки покаже порядкове число першої екстремальної величини m1. Пряма лінія через т1 та інші точки, мають нахил 2d, із якої можна визначити d.


